[Review] PEFT-LoRA
Parameter Efficient Fine-Tuning(PEFT)라 불리는 모델 튜닝 방식에 대해서, 그 중에서도 Alpaca에서도 사용되는 등 가장 널리 알려진 Low-Rank Adaptation of LLM(LoRA)에 대해 정리해보자.
1. Introduction
이제는 하나의 large-scale pre-trained model을 다양한 down-stream task에 활용하기 위해 fine-tuning으로 추가적인 학습을하는 방식은 당연하다. 그러나 시간이 지날수롣 이제는 model, 특히 language model의 size가 너무나도 커져서, 모든 parameter를 fine-tuning 하는 방식은 거의 불가능에 가깝다. GPT-3의 경우 파라미터가 무려 175B. 이거를 전부 다시 학습 시킨다 하면… 미친다
“Adapter Layers Introduce Inference Latency”: 그래서 downstream task를 수행하게 위해 기존에는 pre-trained model weight를 freeze하고 추가적인 module을 학습하는 방식(adapter layer라 부른다)이 활용되었는데, 이는 추가적인 inference latency가 도입되는 단점이 있다.
“Directly Optimizing the Prompt is Hard”: 혹은 prompt tuning, prefix tuning과 같이 input layer activation을 optimizing하는 방식이 있었는데, 이는 모델의 입력 sequence length를 줄여야 하고 효율성과 모델 성능 간의 trade-off를 고려해야한다.
이 때, 저자의 Idea는 “Measuring the Intrinsic Dimension of Objective Landscapes”와 “Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning”의 논문에서 시작되는데. 잘 학습된 model의 weight는 high dimension이라 할지라도, low-intrinsic manifold에 reside한다는 내용이다. 그래서 저자는, “model adaptation 동안 weight 변화 또한 low intrinsic rank이지 않을까?”하는 생각을 한 것이다.
2. LoRA
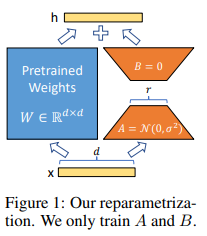
저자가 제안한 방식은 마찬가지로 pre-trained weight를 freeze하면서도, fine-tuning 시 dense layer의 변화를 rank decomposition을 통해 간접적으로 학습하는 것이다. 이 때, 그림과 같이 병렬적으로 학습하여 추가적인 inference latency가 없게 되고, full rank(i.e. d)가 아닌 매우 낮은 rank(r=1~2)에서도 잘 작동하여 storage-/compute-efficient하게 된다. 또한, LoRA는 prefix-tuning과 같은 방식과 전혀 연관이 없기에(orthogonal) 가령 두 방법을 동시에 적용할 수도 있다.
Mathematical Expression
Pre-trained autoregressive language model $P_{\Phi}(y\mid x)$가 주어져있다고 하자. 가령 RoBERTa, DeBERTa, GPT-2/3 같은 일반적인 multi-task learner가 되겠다. 그래서 우리는 이 모델을 downstream task에 적용하게 된다. downstream task의 dataset을 $Z={(x_{i},y_{i})}$라 할 때, full fine-tuning을 한다하면 전체 model의 weight를 업데이트하게 된다. $\Phi_{0}\rightarrow \Phi_{0}+\Delta \Phi$ 일반적으로 하다샆이 log likelihood를 maximize하게 되겠다. \(\underset{\Phi}{max}\sum_{\{x,y\}\in Z}\sum_{t=1}^{\|y\|}log(P_{\Phi}(y_{t}\mid x, y_{<t}))\) 그러나 앞서 말했다 싶이, $\Delta \Phi$는 무려 파라미터가 GPT-3로 치면 175B. 이건 뭐 불가능하다.
그래서 앞에서 잠깐 소개했듯이, 요 $\Delta \Phi$를 훨씬 작은 파라미터 set $\Theta$로 학습하는 것이 parameter-efficient 하겠다. $|\Phi_{0}|\approx 0.01\times |\Theta|$
\[\underset{\Theta}{max}\sum_{\{x,y\}\in Z}\sum_{t=1}^{\|y\|}log(P_{\Phi_{0}+\Delta \Phi(\Theta)}(y_{t}\mid x, y_{<t}))\]그래서 $\Delta \Phi(\Theta)$를 어떻게 효과적으로 학습하는가. 우선, network에 있는 dense layer는 거의 다 matrix multiplication $(h=W_{0}x)$을 수행하고 있다. 여기서 $W_{0}$를 $W_{0}+\Delta W$로 update 하면서 $\Delta W$를 학습할 건데, 저자는 이 변화량 또한 low subspace에 존재할 것이라 가정하여 low-rank decomposition을 통해 간접적으로 이를 학습한다. 즉, $W_{0}\in \mathbb{R}^{d\times k}$라 할 때, $W_{0}+\Delta W=W_{0}+BA\;\;where\;B\in \mathbb{R}^{d\times r},\,A\in \mathbb{R}^{r\times k},r\ll min(d,k)$로 $W_{0}$는 freeze한 채 B와 A를 학습하는 것이다. 논문에서 A와 B의 initialization은 A는 random Gaussian, B는 zero로 $(\Delta W=0)$하고, $\Delta W$를 scaling도 해주었다. 이 부분이 정확히 이해가 안 된다.. scaling facotr가 learning rate tuning과 거의 유사하다는데 무슨 말이지
위 방식에 따르면, Full-Fine tuning은 rank r을 $W_{0}$의 rank로 setting하는 것과 거의 동일하다. 그리고 inference 시에는 $W=W_{0}+BA$이기에 따로 추가적인 computation 없이 그냥 $Wx$를 계산하므로, additional inference latency가 없다. 여러 downstream task에 활용하려면, 다시 $W$에서 $BA$를 빼고 추가로 $B’A’$를 학습해주면 되겠다.
그렇다면 Transformer의 self-attention module에도 동일하게 적용할 수 있다. SA block에는 총 4개$(W_{q},W_{k},W_{v},W_{o}\in \mathbb{R}^{d_{model}\times d_{model}})$의 weight가 있고, Q,K,V가 주어져있을 때 output은 다음과 같았다. (논문에서처럼 Multi-head가 아닌 single-head를 가정하자.)
\[\mathrm{SelfAttention}(Q,K,V)=\mathrm{Attention}(QW_{q},KW_{k},VW_{v})W_{o} \\ where\;\;\mathrm{Attention}(Q,K,V)=\mathrm{softmax}(\frac{QK^{T}}{\sqrt{d_{model}}})V\]물론 Transformer block에 MLP도 있지만 MLP module은 freeze하고, attention weight만 adapting 하였다. 여기서도 어떤 weight matrix를, rank r을 얼마로 해서 adapting 할 것인지 여러 choice가 있는데. 아래 실험에서 확인하자.
3. Experiment
Baselines
- FT: full fine-tuning을 뜻한다.
- FT Top2: 마지막 2개의 layer만 fine-tuning하고 나머지는 freeze하는 방식을 말한다.
- BitFit: bias vector만을 학습하고 나머지는 freeze하는 방식을 말한다.
- PreEmbed: input token에 추가적인 special token을 넣어주면서 이를 학습하고 모델의 파라미터는 freeze한다. prompt의 앞에 추가하기도(prefixing, $l_{p}$개의 token), 뒤에 추가하기도(infixing, $l_{i}$개의 token) 하였다. $|\Theta |=d_{model}\times (l_{p}+l_{i})$
- PreLayer: Transformer layer(총 L개)를 거친 뒤의 activation 전부를 학습한다. $|\Theta |=L\times d_{model}\times (l_{p}+l_{i})$
- AdapterH: bias를 포함한 2개의 FC(중간에 nonlinear activation 포함) adapter를 self-attention과 residual connection 사이에 추가하였다.
- AdapterL: 동일한 adapter를 MLP 이후, LayerNorm 이후에 추가하였다.
- AdapterP: Pfeiffer et al. (2021)의 “AdapterFusion: Non-Destructive Task Composition for Transfer Learning” 논문에서 제안한 방식.
- AdapterD: Rücklé et al. (2020)의 “Adapterdrop: On the efficiency of adapters in transformers” 논문에서 제안한 방식. (6~9 모두, \(\|\Theta \|=\hat{L}_{Adpt}\times (2\times d_{model}\times r+r+d_{model})+2\times \hat{L}_{LN}\times d_{model}\), \(\hat{L}_{Adpt}\)는 adapter layer 개수, \(\hat{L}_{LN}\)는 AdapterL에서 처럼 trainable LayerNorm 개수)
- LoRA: \(\hat{L}_{LoRA}\)개의 weight matrix에 위에서 설명한 LoRA를 적용. \(\|\Theta \|=2\times \hat{L}_{LoRA}\times d_{model}\times r\)
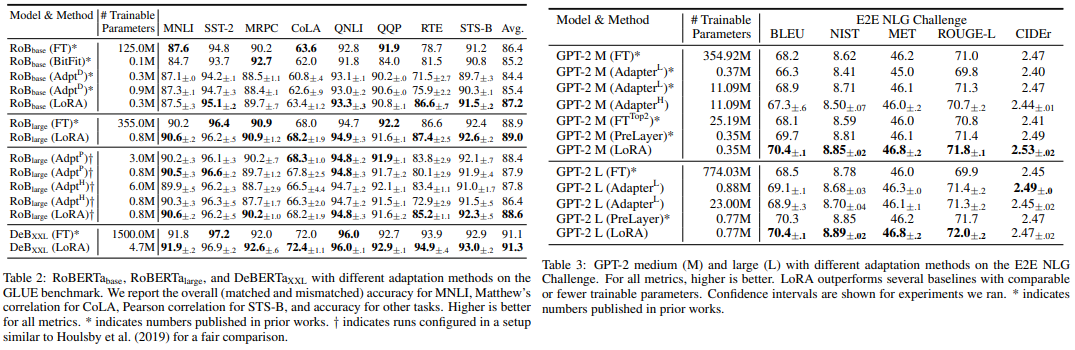
전체적으로 봤을 때 Trainable Parameter 수를 타 방식에 비해 훨씬 줄였음에도, GLUE benchmark에서 Avg. score가 좋게 나왔다.
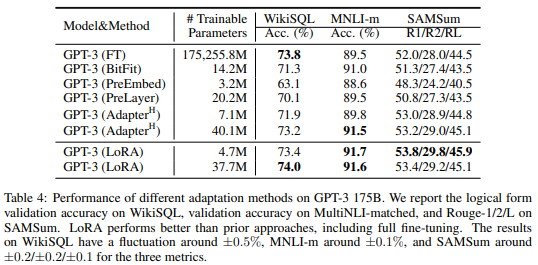
엄청 큰 모델에서도 좋은 성능을 보여준다. 표에서 위 LoRA는 $r_{v}=2$ 세팅이고, 아래 LoRA는 $r_{q}=r_{k}=r_{v}=r_{o}=4$ 세팅이다.
Ablation Studies
◼ Pre-trained Transformer에 어떤 weight matrice를 adapt해야 되는가?
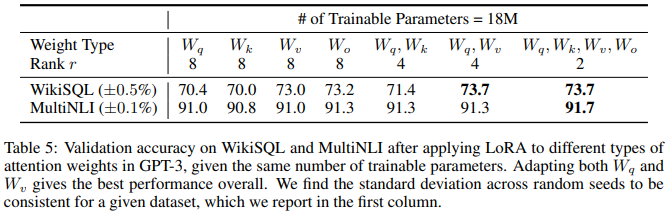
같은 파라미터 수 대비 모든 weight matrice에 적용할 경우 rank가 줄어든다. 그럼에도 불구하고 모든 weight matrice에 적용하는 것이 성능이 좋으며, 특히 query와 value matrix에 적용할 때 가장 좋은 성능을 보였다. 이를 통해서, rank가 큰 하나의 weight를 adapt하기 보다는 rank가 작아도 여러개의 weight matrices를 adapt하는 것이 좋음을 알 수 있다.
◼ rank r은 어떻게 세팅해야 되는가?
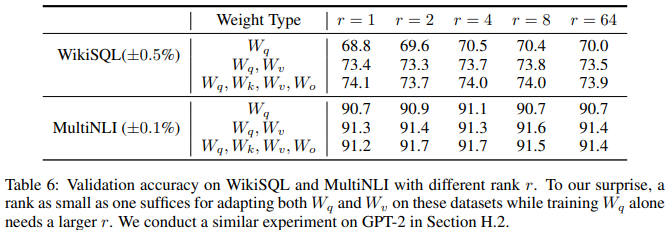
저자가 세운 가정에 일치하는데, r이 매우 작아도 충분하다고 제안하고 있다. 다만 항상 그런 것은 아니라면서, 예를 들어 pre-trained model이 영어 모델인데 down-stream task가 중국어 관련일 때는 아예 retraining(즉, r을 full rank로) 하는 것이 더 좋을수도 있다고 경고하고 있다. 그러면서 r의 크기에 따라 학습된 subspace의 유사성을 Grassmann distance 기반으로 정량화 하였는데, 행렬의 SVD를 통한 right-singular unitary 행렬에서 rank 8과 rank 64로 학습한 top 1 singular vector의 유사도가 0.5 이상임을 확인하였다. 따라서 매우 낮은 rank가 가능하다는 걸 보였다.
◼ Adaptation Matrix $\Delta W$는 $W$와 어떤 관계인가?

$\Delta W$가 $W$와 highly correlated 되어있는지, 그리고 $\Delta W$가 얼마나 큰지 비교하였다. 우선, Random에 비해 adaptation matrix는 weight와 correlation이 더 높다는 것을 볼 수 있다. 이는 W에 있던 특징을 adaptation matrix가 더 강화한다고 볼 수 있다. 그리고 adaptation matrix는 W의 top singular direction을 반복하지 않고 W에 강화되지 않았던 방향을 강화한다. 그리고 amplification factor가 높다. (6.91/0.32=21.5) 이를 통해 low-rank adaptation matrix는 pre-trained model에서는 별로 강조되지 않았던 특징들을 down-stream task에 맞게 강조한다고 볼 수 있겠다.
4. Implementation
Transformer Layer 말고 linear layer에 간단히 구현해보자. 왜냐하면 HuggingFace에서 PEFT library에서 다 해줘서…
참고로 @는 tensor간 multiplication을 의미한다.
# https://github.com/microsoft/LoRA/blob/main/loralib/layers.py
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
class LoRALayer():
def __init__(
self,
r: int,
lora_alpha: int,
lora_dropout: float,
merge_weights: bool,
):
# Rank & Scaling Factor
self.r = r
self.lora_alpha = lora_alpha
# Optional dropout
if lora_dropout > 0.:
self.lora_dropout = nn.Dropout(p=lora_dropout)
else:
self.lora_dropout = lambda x: x
# Mark the weight as unmerged
self.merged = False
self.merge_weights = merge_weights
class Linear(nn.Linear, LoRALayer):
# LoRA implemented in a dense layer
def __init__(
self,
in_features: int,
out_features: int,
r: int = 0,
lora_alpha: int = 1,
lora_dropout: float = 0.,
fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
merge_weights: bool = True,
**kwargs
):
nn.Linear.__init__(self, in_features, out_features, **kwargs)
LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout,
merge_weights=merge_weights)
self.fan_in_fan_out = fan_in_fan_out
# Actual trainable parameters
if r > 0:
self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))
self.scaling = self.lora_alpha / self.r
# Freezing the pre-trained weight matrix
self.weight.requires_grad = False
self.reset_parameters()
if fan_in_fan_out:
self.weight.data = self.weight.data.transpose(0, 1)
def reset_parameters(self):
nn.Linear.reset_parameters(self)
if hasattr(self, 'lora_A'):
# initialize A the same way as the default for nn.Linear and B to zero
nn.init.kaiming_uniform_(self.lora_A, a=math.sqrt(5))
nn.init.zeros_(self.lora_B)
def train(self, mode: bool = True):
def T(w):
return w.transpose(0, 1) if self.fan_in_fan_out else w
nn.Linear.train(self, mode)
if mode:
if self.merge_weights and self.merged:
# Make sure that the weights are not merged
if self.r > 0:
self.weight.data -= T(self.lora_B @ self.lora_A) * self.scaling
self.merged = False
else:
if self.merge_weights and not self.merged:
# Merge the weights and mark it
if self.r > 0:
self.weight.data += T(self.lora_B @ self.lora_A) * self.scaling
self.merged = True
def eval(self):
def T(w):
return w.transpose(0, 1) if self.fan_in_fan_out else w
nn.Linear.eval(self)
if self.merge_weights and not self.merged:
# Merge the weights and mark it
if self.r > 0:
self.weight.data += T(self.lora_B @ self.lora_A) * self.scaling
self.merged = True
def forward(self, x: torch.Tensor):
def T(w):
return w.transpose(0, 1) if self.fan_in_fan_out else w
if self.r > 0 and not self.merged:
result = F.linear(x, T(self.weight), bias=self.bias)
result += (self.lora_dropout(x) @ self.lora_A.transpose(0, 1) @ self.lora_B.transpose(0, 1)) * self.scaling
return result
else:
return F.linear(x, T(self.weight), bias=self.bias)
HuggingFace PEFT
[[HuggingFace PEFT LoRA]] (https://huggingface.co/docs/peft/conceptual_guides/lora)
큰 틀은 공식문서에 나와있는 단계대로 하면 된다.
As with other methods supported by PEFT, to fine-tune a model using LoRA, you need to: 1. Instantiate a base model. 2. Create a configuration (LoraConfig) where you define LoRA-specific parameters. 3. Wrap the base model with get_peft_model() to get a trainable PeftModel. 4. Train the PeftModel as you normally would train the base model.
여기서 LoraConfig는 rank, target_modules(ex:attention block), alpha, bias 등을 포함하고 있다.
from peft import LoraConfig, get_peft_model
from huggingface_hub import login
login()
# 1. Dataset
from datasets import load_dataset
dataset = load_dataset("food101", split="train[:5000]")
model_checkpoint = "google/vit-base-patch16-224-in21k"
labels = dataset.features["label"].names
label2id, id2label = dict(), dict()
for i, label in enumerate(labels):
label2id[label] = i
id2label[i] = label
# Using the image_processor, prepare transformation functions for the datasets.
# These functions will include data augmentation and pixel scaling:
from transformers import AutoImageProcessor
image_processor = AutoImageProcessor.from_pretrained(model_checkpoint)
from torchvision.transforms import (
CenterCrop,
Compose,
Normalize,
RandomHorizontalFlip,
RandomResizedCrop,
Resize,
ToTensor,
)
normalize = Normalize(mean=image_processor.image_mean, std=image_processor.image_std)
train_transforms = Compose(
[
RandomResizedCrop(image_processor.size["height"]),
RandomHorizontalFlip(),
ToTensor(),
normalize,
]
)
val_transforms = Compose(
[
Resize(image_processor.size["height"]),
CenterCrop(image_processor.size["height"]),
ToTensor(),
normalize,
]
)
def preprocess_train(example_batch):
"""Apply train_transforms across a batch."""
example_batch["pixel_values"] = [train_transforms(image.convert("RGB")) for image in example_batch["image"]]
return example_batch
def preprocess_val(example_batch):
"""Apply val_transforms across a batch."""
example_batch["pixel_values"] = [val_transforms(image.convert("RGB")) for image in example_batch["image"]]
return example_batch
splits = dataset.train_test_split(test_size=0.1)
train_ds = splits["train"]
val_ds = splits["test"]
train_ds.set_transform(preprocess_train)
val_ds.set_transform(preprocess_val)
# 2. Model
def print_trainable_parameters(model):
trainable_params = 0
all_param = 0
for _, param in model.named_parameters():
all_param += param.numel()
if param.requires_grad:
trainable_params += param.numel()
print(
f"trainable params: {trainable_params} || all params: {all_param} || trainable%: {100 * trainable_params / all_param:.2f}"
)
from transformers import AutoModelForImageClassification, TrainingArguments, Trainer
model = AutoModelForImageClassification.from_pretrained(
model_checkpoint,
label2id=label2id,
id2label=id2label,
ignore_mismatched_sizes=True, # provide this in case you're planning to fine-tune an already fine-tuned checkpoint
)
print_trainable_parameters(model)
"trainable params: 85876325 || all params: 85876325 || trainable%: 100.00"
# 3. Main! PEFT
from peft import LoraConfig, get_peft_model
config = LoraConfig(
r=16,
lora_alpha=16,
target_modules=["query", "value"],
lora_dropout=0.1,
bias="none",
modules_to_save=["classifier"], # modules_to_save: List of modules apart from LoRA layers
# to be set as trainable and saved in the final checkpoint. These typically include
# model’s custom head that is randomly initialized for the fine-tuning task.
)
lora_model = get_peft_model(model, config)
print_trainable_parameters(lora_model)
"trainable params: 667493 || all params: 86466149 || trainable%: 0.77"
from transformers import TrainingArguments, Trainer
model_name = model_checkpoint.split("/")[-1]
batch_size = 16
args = TrainingArguments(
f"{model_name}-finetuned-lora-food101",
remove_unused_columns=False,
evaluation_strategy="epoch",
save_strategy="epoch",
learning_rate=5e-3,
per_device_train_batch_size=batch_size,
gradient_accumulation_steps=4,
per_device_eval_batch_size=batch_size,
fp16=True,
num_train_epochs=5,
logging_steps=10,
load_best_model_at_end=True,
metric_for_best_model="accuracy",
push_to_hub=True,
label_names=["labels"],
)
import numpy as np
import evaluate
metric = evaluate.load("accuracy")
def compute_metrics(eval_pred):
"""Computes accuracy on a batch of predictions"""
predictions = np.argmax(eval_pred.predictions, axis=1)
return metric.compute(predictions=predictions, references=eval_pred.label_ids)
import torch
def collate_fn(examples):
pixel_values = torch.stack([example["pixel_values"] for example in examples])
labels = torch.tensor([example["label"] for example in examples])
return {"pixel_values": pixel_values, "labels": labels}
trainer = Trainer(
lora_model,
args,
train_dataset=train_ds,
eval_dataset=val_ds,
tokenizer=image_processor,
compute_metrics=compute_metrics,
data_collator=collate_fn,
)
train_results = trainer.train()
trainer.evaluate(val_ds)
혹은 그냥 다른 사람(아마 공식 repo인거 같은데)이 한 것 가져와도 된다.
repo_name = f"sayakpaul/vit-base-patch16-224-in21k-finetuned-lora-food101"
from peft import PeftConfig, PeftModel
config = PeftConfig.from_pretrained(repo_name)
# 1. Dataset
from datasets import load_dataset
dataset = load_dataset("food101", split="train[:5000]")
model_checkpoint = "google/vit-base-patch16-224-in21k"
labels = dataset.features["label"].names
label2id, id2label = dict(), dict()
for i, label in enumerate(labels):
label2id[label] = i
id2label[i] = label
from transformers import AutoModelForImageClassification
model = AutoModelForImageClassification.from_pretrained(
config.base_model_name_or_path,
label2id=label2id,
id2label=id2label,
ignore_mismatched_sizes=True, # provide this in case you're planning to fine-tune an already fine-tuned checkpoint
)
# Load the LoRA model
inference_model = PeftModel.from_pretrained(model, repo_name)
from PIL import Image
import requests
url = "https://huggingface.co/datasets/sayakpaul/sample-datasets/resolve/main/beignets.jpeg"
image = Image.open(requests.get(url, stream=True).raw)
from transformers import AutoImageProcessor
image_processor = AutoImageProcessor.from_pretrained(repo_name)
encoding = image_processor(image.convert("RGB"), return_tensors="pt")
import torch
with torch.no_grad():
outputs = inference_model(**encoding)
logits = outputs.logits
predicted_class_idx = logits.argmax(-1).item()
print("Predicted class:", inference_model.config.id2label[predicted_class_idx])
5. Summary

큰 pre-trained 모델을 downstream task에 fine-tuning 할 때, 기존 weight는 freeze하고 추가적으로 low rank adaptation matrix를 parallel하게 학습하여 적은 양의 파라미터로 모델을 튜닝함과 동시에 추가적인 inference latency는 없도록 하였다.
Reference
Websites
[사이트 출처 1] (https://huggingface.co/docs/peft/index)
[사이트 출처 2] (https://www.sktenterprise.com/bizInsight/blogDetail/dev/4222)
[사이트 출처 3] (https://github.com/microsoft/LoRA/blob/main/loralib/layers.py)
Papers
[1] Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685.
댓글남기기