Diffusion Model의 기본 Architecture는 DDPM 때 부터 U-Net을 주로 써왔다. 그러나, “굳이 U-Net?”이라는 의문이 들 수 있기에. Transformer를 사용한 Diffusion Transformer, DiT 논문을 살펴보자. 정확한 논문 이름은 Scalable Diffusion Models with Transformers.

1. Introduction

Transformer & ViT

[My Transformer Review]

Vision Transformer(ViT)에 대한 내용을 아직 글을 작성하지는 않았지만, 워낙에 유명하기도 하고 Transformer 구조와 크게 다른 것이 없기에. 일단 큰 틀은 아래 사진과 같다.

ViT

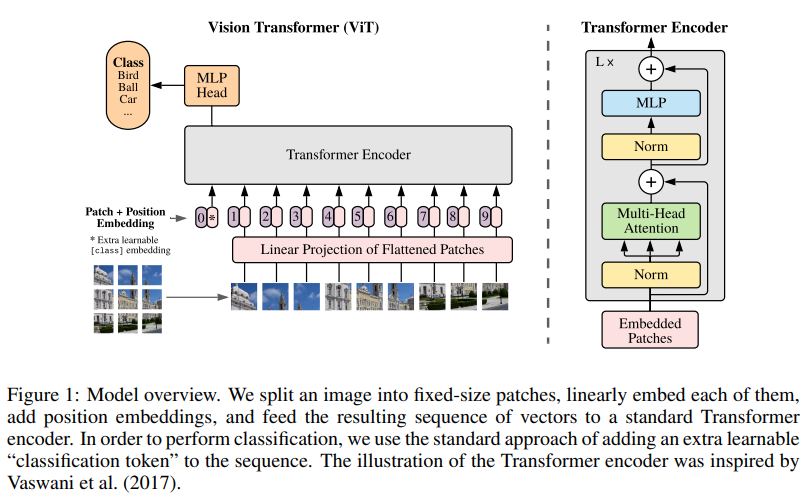
논문 제목처럼 Image를 PxP patch로 나눈 뒤 이 각각의 patch를 Transformer에서 하나의 단어로 취급하는 구조이다. Position Embedding도 Transformer에서 각 단어가 문장에서 몇 번째 위치인지에 대한 정보를 담고 있듯이 ViT에서는 각 patch가 image의 어떤 위치에 있었는지에 대한 정보를 담고 있고, 학습해도 되고 sinusoidal embedding으로 encoding해도 된다. BERT에서 idea를 가져와서 BERT에서의 CLS 토큰 처럼 추가로 학습할 0번 토큰을 넣어주고 있다.

ViT 모델 구조에서 hyperparameter로는 Transformer Encoder Layer 개수, Hidden dimension size, Attention 시 head 수, MLP size 등에 따라 Base, Large, Huge 모델로 나뉜다.

DM / LDM

[My Diffusion Review]

Forward Process \(q(X_{t}\mid X_{0})=N(X_{t}:\sqrt{\overline{\alpha_{t}}}X_{0},(1-\overline{\alpha_{t}})I)\;where\;\alpha_{t}=1-\beta_{t},\overline{\alpha_{t}}=\prod_{i=1}^{t}\alpha_{i}\)를 통해 initial data에 noise를 단계적으로 넣어주고, reverse process \(q(X_{t-1}\mid X_{t})\)의 분포를 따라 noise를 제거해주면 되기에 이를 \(p_{\theta}(X_{t-1}\mid X_{t})=N(\mu_{\theta}(x_{t}),\Sigma_{\theta}(x_{t}))\)로 네트워크를 통해 학습한다. 학습할 때 Loss는

\[\begin{align*} V_{vlb}&:=L_{0}+L_{1}+...+L_{T-1}+L_{T} \\ L_{0}&:=-log\,p_{\theta}(x_{0}\mid x_{1}) \\ L_{t-1}&:=D_{KL}(q(x_{t-1}\mid x_{t},x_{0}) \,||\,p_{\theta}(x_{t-1}\mid x_{t})) \\ L_{T}&:=D_{KL}(q(x_{T}\mid x_{0})\,||\,p(x_{T})) \end{align*}\]

로, 여기서 DDPM에서는 \(p_{\theta}(X_{t-1}\mid X_{t})\)의 분산은 학습하지 않고 평균을 “더해지는 noise를 학습함”으로써 학습하였다: \(\mu_{\theta}(x_{t},t)=\frac{1}{\alpha_{t}}(x_{t}-\frac{\beta_{t}}{\sqrt{1-\overline{\alpha_{t}}}} \epsilon_{\theta}(x_{t},t))\) 또한 Loss를 \(L_{simple}=\mathbb{E}_{t,x_{0},\epsilon}[\left \| \epsilon-\epsilon_{\theta}(x_{t},t) \right \|^{2}]\)로 간단히 하였다.

Improved DDPM 논문에서 noise scheduling만 다루었었는데, 해당 논문에서는 평균뿐만 아니라 분산도 학습하는 것 또한 다루고 있다. simple loss term만으로 평균(정확히는 noise)을 학습하고, stop-gradient를 이용해 full loss term으로 분산을 학습하는 방식이다. Diffusion Transformer 논문에서도 동일하게 이와 같은 방식으로 학습을 진행하였다.

Latent Diffusion(Stable diffusion) Model도 Diffuison 리뷰 글에서 다루었는데, Diffusion Transformer 논문도 LDM의 방식을 그대로 따른다. 1/8배 downsample하는 pre-trained VAE encoder를 거친 뒤 latent 단에서의 diffusion을 학습하고, 이를 다시 pre-trained VAE decoder를 거치는 방식이다.

Classifier Free Guidance

역시 Diffusion Review 글에서 잠깐 다루었었는데, \(\varepsilon_{\theta}(x_{t})-s\nabla_{x_{t}}logp_{\phi}(y \mid x_{t})\)로 나타나는 Classifier Guidance에서 추가적인 Classifier 학습 없이 동일한 효과를 낼 수 있는 방법이 CFG였다. Bayes Rule에 따라 \(\nabla_{x_{t}}logp_{\phi}(y \mid x_{t})\propto \nabla_{x_{t}}logp_{\phi}(x_{t} \mid y)-\nabla_{x_{t}}logp_{\phi}(x_{t})\)를 이용한 것으로, \(\hat \varepsilon_{\theta}(x_{t},c)=\varepsilon_{\theta}(x_{t},\phi)-s\nabla_{x_{t}}logp_{\phi}(y \mid x_{t})\propto \varepsilon_{\theta}(x_{t},\phi)+s(\varepsilon_{\theta}(x_{t},c)-\varepsilon_{\theta}(x_{t},\phi))\)가 되겠다. (이 때 \(\phi\)는 빈 text embedding)

Diffusion Transformer 에서도 마찬가지로 Classifier Free Guidance를 통한 Class conditioned Image generation 결과를 보여주고 있다.

Architecture Complexity - Gflops

Architecture가 얼마나 복잡한지 나타내는 직관적인 지표로는 모델의 parameter 개수가 떠오를 수 있겠지만, 이는 complexity로써의 지표에 적합하지 않다. 가령 예를 들면 ViT-Base 모델에서 patch size 16과 patch size 32는 모델 파라미터 수는 같지만, GFLOPs가 거의 4배 차이가 난다. 여기서 Gflops는 floating point operations, 부동소수점 연산량으로 곱하기 더하기 등의 연산량 총 개수를 뜻한다. 그래서 Diffusion Transformer에서는 이 Gflops 수치를 통해 모델이 복잡할수록 성능이 좋아진다는 것을 보여주고 있다. 물론 막연하게 Gflops만 올리는 것이 아니라 최소한으로 올리면서도 성능은 좋은 방식을 제시하는데, 이제 이에 대해서 알아보자.

2. Design

Patchify

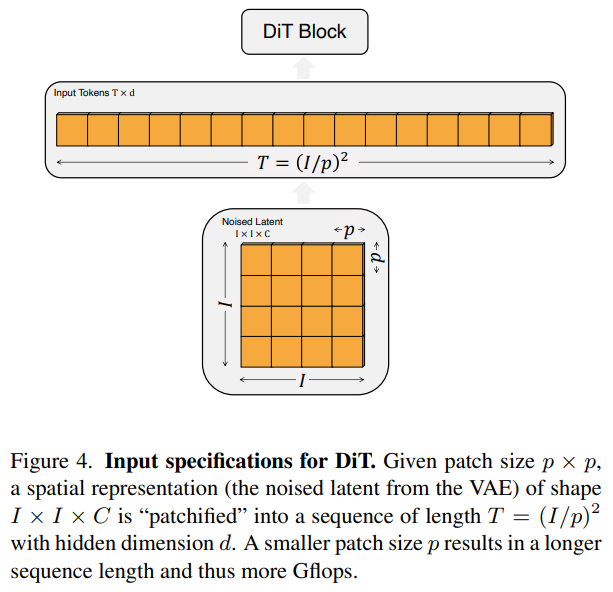
Patchify

ViT와 동일하게 input으로 들어오는 latent (image가 아니다, Latent diffusion model 처럼 VAE encoder를 거친 latent가 DiT의 input이 된다.) IxIxC를 patch로 나누어 Txd로 보낸다. 이 때 T는 전체 patch 개수가 되겠고, d는 ViT와 동일하게 hidden dimension size가 되겠다. 실험에서 p는 hyperparameter로 2,4,8 이렇게 3가지 경우를 두었다. hidden dimension은 model size에서 다루자.

Block design

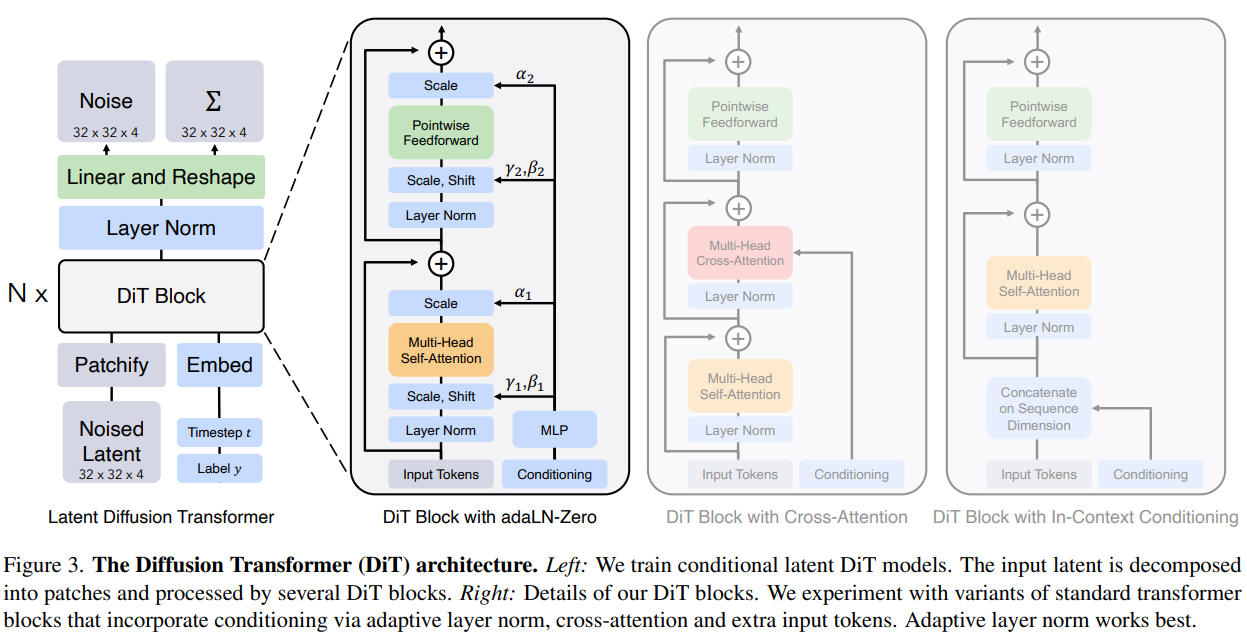
DiTBlock

기본 틀은 LDM과 동일하게 diffusion timestep embedding t과 class label embedding c을 condition으로, 그리고 patchify 된 latent를 input으로 받아서 N개의 DiT Block(Transformer encoder라 생각하면 된다.)을 거치고 이후 LN+(Linear&rearrange)(Transformer decoder라 생각하면 된다.)를 거쳐 latent 단에서의 평균(noise)과 분산을 학습한다. 논문에서 채택한 DiT Block 구조는 4가지가 있다.

  1. In-Context Conditioning: t, c를 input sequence의 additional token으로 취급한다. BERT/ViT에서 CLS 토큰과 유사한 역할.
  2. Cross-Attention: Cross-Attention Layer를 MHSA와 MLP 사이에 추가하여 t, c를 K, V로 준다. LDM에서 Cross-attention을 그대로 활용했다.
  3. adaLN: LN을 adaptive LN으로 변경하였다. (Transformer decoder에 있는 LN 또한 adaLN으로 바꾸었다) scaling factor \(\gamma\)와 shift factor \(\beta\)를 이용해 \(\gamma \cdot LN(x)+\beta\)로 구해지는데, 이 때 이 두개의 factor는 t, c를 MLP를 거쳐 얻는다. 따라서 학습가능하게 되는 구조.
  4. adaLN-Zero: zero-initializing이 도움이 된다는 다른 논문으로부터 아이디어를 얻어, 위 3. adaLN에서 scaling factor \(\alpha\)를 추가한 뒤 zero-initailzied한다.

adaLN에 대해 잘 설명해주는 그림이 DiverGAN이라는 논문에 실려있어서 가져왔다. 아래 그림은 심지어 Instance Norm과 합작하는데, 일단 무시하자. 그림에서 sentence vector로 나타난 것을 time/class embedding이라 생각하면 되고, 이것으로부터 FC를 거쳐 scaling/shifting factor를 얻는다. 그러면 LayerNorm을 거친 기존 결과에다가 두 factor를 고려해주는 것이다.

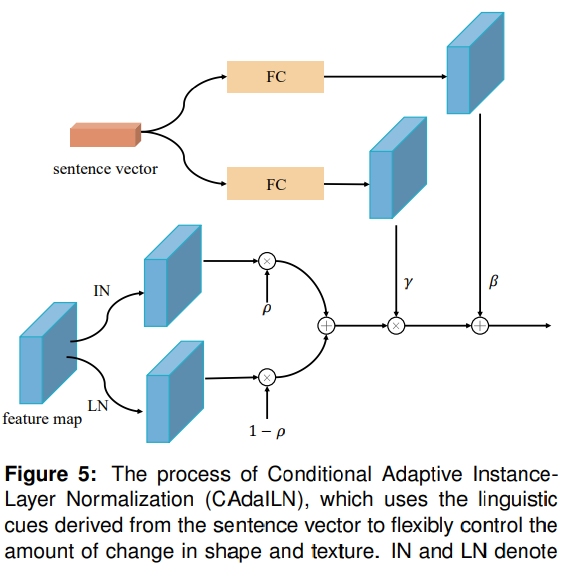
CadaILN

DiT 공식 github에서 구현된 것을 보면 좀 더 이해하기 쉬웠다.

# Copied from https://github.com/facebookresearch/DiT/blob/main/models.py
class DiTBlock(nn.Module):
    """
    A DiT block with adaptive layer norm zero (adaLN-Zero) conditioning.
    """
    def __init__(self, hidden_size, num_heads, mlp_ratio=4.0, **block_kwargs):
        super().__init__()
        self.norm1 = nn.LayerNorm(hidden_size, elementwise_affine=False, eps=1e-6)
        self.attn = Attention(hidden_size, num_heads=num_heads, qkv_bias=True, **block_kwargs)
        self.norm2 = nn.LayerNorm(hidden_size, elementwise_affine=False, eps=1e-6)
        mlp_hidden_dim = int(hidden_size * mlp_ratio)
        approx_gelu = lambda: nn.GELU(approximate="tanh")
        self.mlp = Mlp(in_features=hidden_size, hidden_features=mlp_hidden_dim, act_layer=approx_gelu, drop=0)
        self.adaLN_modulation = nn.Sequential(
            nn.SiLU(),
            nn.Linear(hidden_size, 6 * hidden_size, bias=True)
        )

    def forward(self, x, c):
        shift_msa, scale_msa, gate_msa, shift_mlp, scale_mlp, gate_mlp = self.adaLN_modulation(c).chunk(6, dim=1)
        x = x + gate_msa.unsqueeze(1) * self.attn(modulate(self.norm1(x), shift_msa, scale_msa))
        x = x + gate_mlp.unsqueeze(1) * self.mlp(modulate(self.norm2(x), shift_mlp, scale_mlp))
        return x

# Skipped...
# In DiT,
# Zero-out adaLN modulation layers in DiT blocks:
    for block in self.blocks:
        nn.init.constant_(block.adaLN_modulation[-1].weight, 0)
        nn.init.constant_(block.adaLN_modulation[-1].bias, 0)

Model size

DiT Size

Hyperparameter로는 또 DiT Encoder Layer 개수, patchify 시 hidden dimension, 그리고 self-attention시 multi-head 개수 등이 있을 텐데, 이를 ViT에서의 notation과 동일하게 Small, Base, Large, XLarge로 구분하였다.

결과적으로는 p=2,4,8, 그리고 S,B,L,XL 이렇게 총 3x4=12개의 모델이 있겠다. Block Design 4가지도 포함하면 총 48개의 모델인데, adaLN-Zero Block이 성능이 잘 나와서 이것만 채택했다. block type 별 성능은 아래 실험 결과에서 살펴보자. 논문에서 모델을 위 구조로 부른다: DiT-(Model Size)/(Patch Size)-G(CFG used or not). 예를 들어 바로 아래에서 살펴볼 DiT-XL/2-G (cfg=1.50)은 DiT XL 구조에 patch size는 가장 작은 2로 설정하였고, Classifier free guidance scale factor를 1.50으로 설정하여 활용하였다는 것이다.

3. Experiment Results

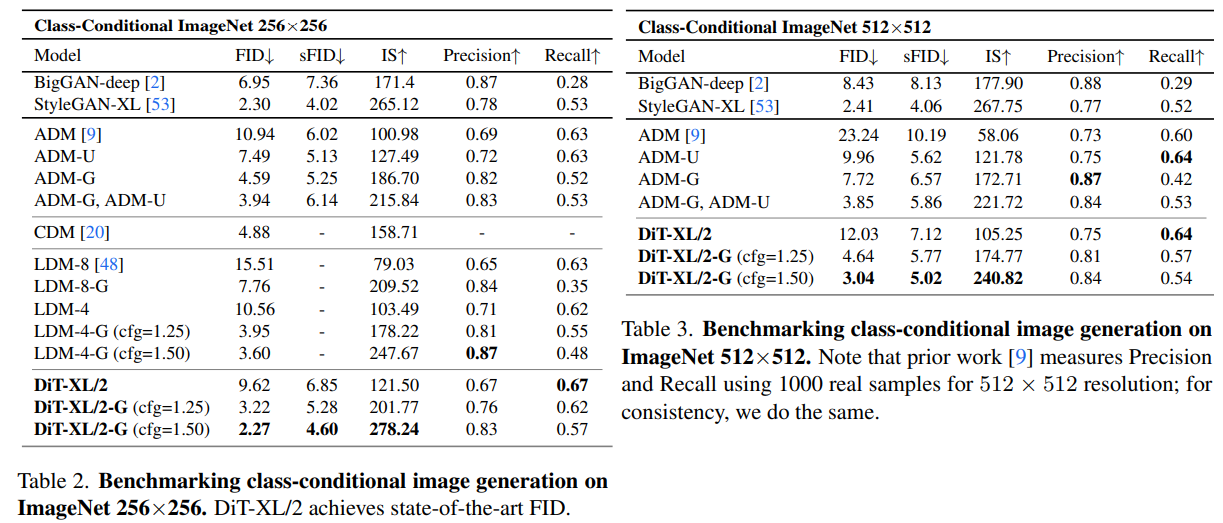
DiT Result

Class-conditional Image generation task에서 256x256, 512x512 2개의 resolution에 대한 결과이다. 당연하게도 가장 좋다고 얘기하고 있다.

Ablation Studies

◼ Which Block Design performs better?

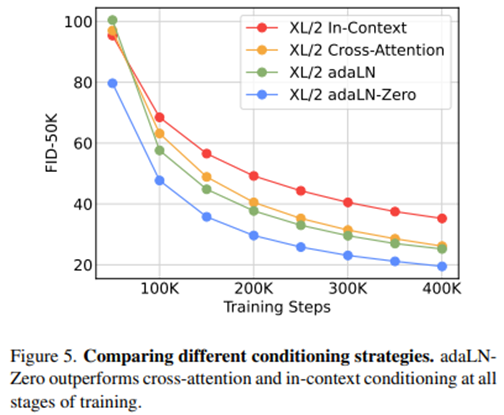
DiT Ablation 0

DiT-XL/2 model 기준 In-context block는 Gflops=119.4, Cross-attention block은 Gflops=137.6, adaLN과 adaLN-Zero block은 Gflops=118.6이라고 한다. 그랬을 때 그림에서 볼 수 있다 싶이 adaLN-Zero가 가장 FID가 낮은데, Gflops는 나머지 2개에 비해 가장 작다. 막연하게 Gflops를 올린게 아니라 compute-efficient하면서도(?) FID는 낮게 나오는 좋은 결과라 볼 수 있겠다.

◼ Which Model size/Patch size performs better?

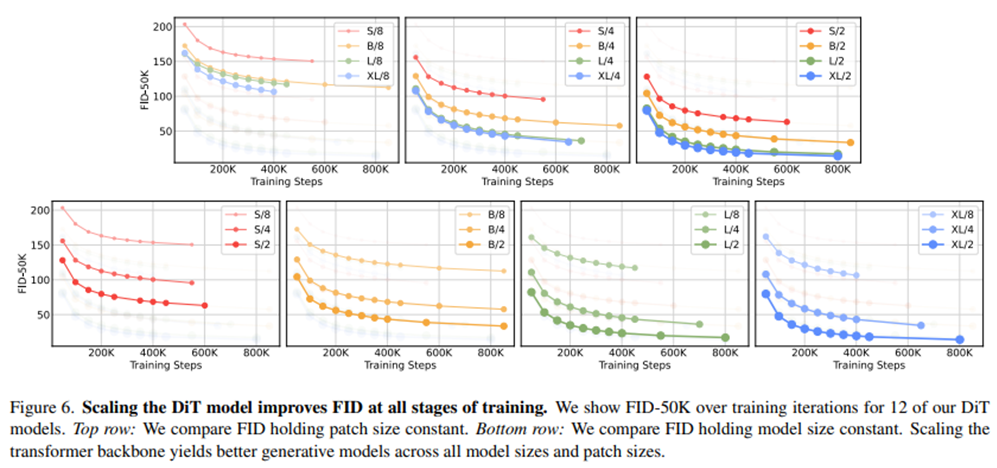
DiT Ablation 1

위 그림에서 top row를 통해 Patch Size가 같을 때 Model Size가 클 수록 FID가 낮음을 확인할 수 있고, botton row를 통해 Model Size가 같을 때 Patch Size가 작을 수록 FID가 낮음을 확인할 수 있다. 아래 그림에서 왼쪽이 정성적인 분석인데, 실제로 transformer size를 키우고 patch size를 작게 한 오른쪽 아래 그림이 가장 퀄리티가 좋은게 한 눈에 보인다.

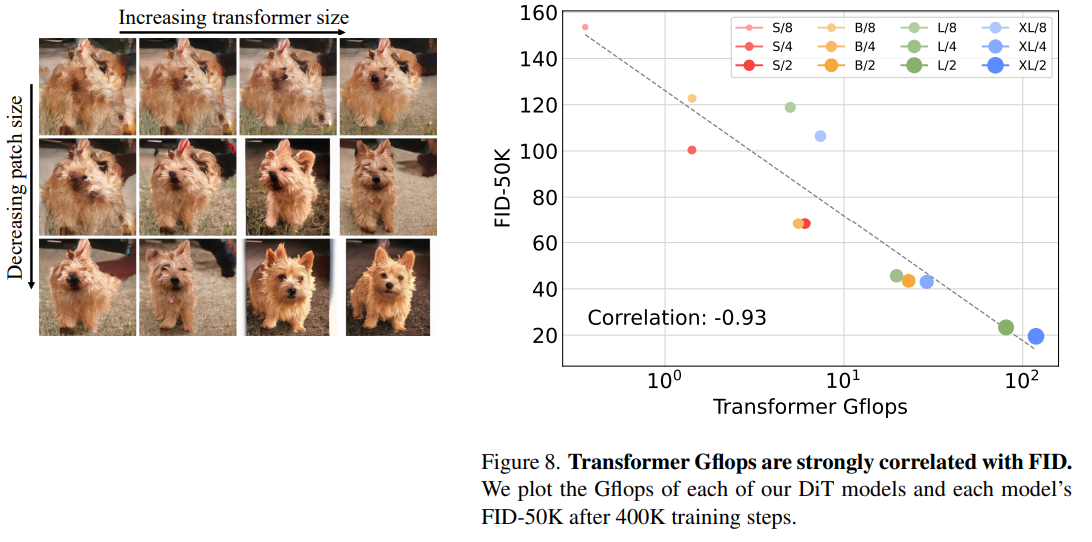
DiT Ablation 1/2

◼ Does higher Gflops really yields better performance?

ViT와 유사하게 Model Size가 동일할 때 Patch size를 작게 하면 parameter 수는 변하지 않고 (오히려 살짝 감소) Gflops만 증가하게 된다. 저자는 정말로 Gflops와 FID가 상관관계가 있는지 확인했을 때, Correlation이 0.93으로 매우 높은 것을 확인하였다.

◼ Isn’t large model too compute-inefficient?

◼ How about sampling steps: smaller DiT w/ more sampling steps?

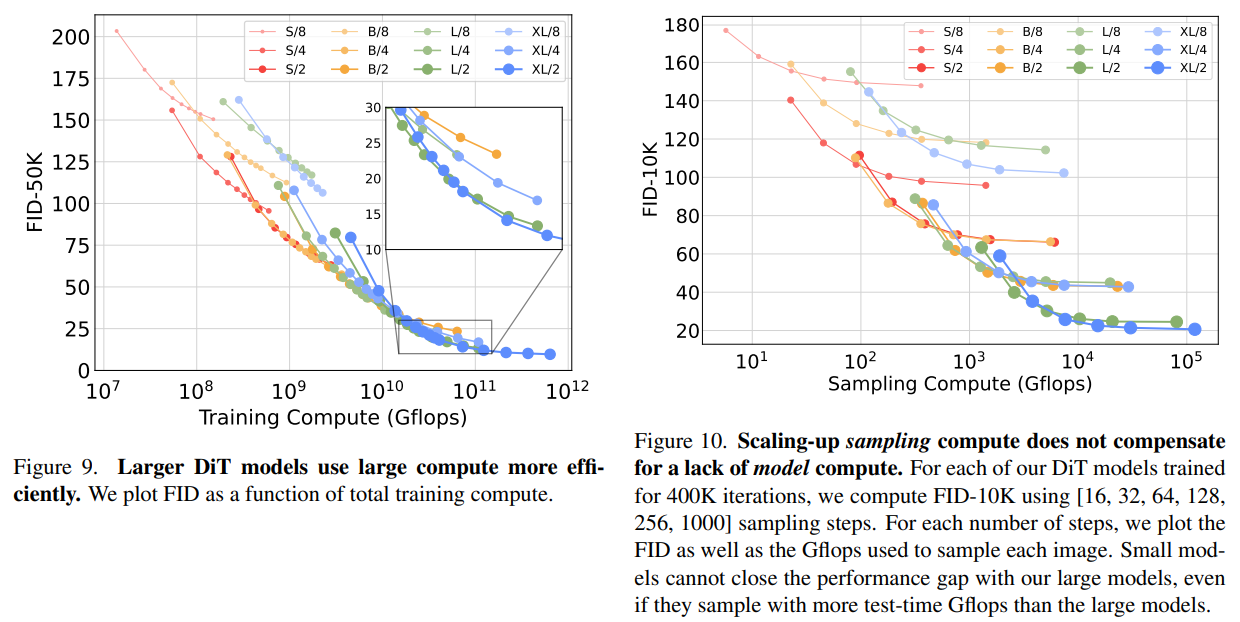
DiT Ablation 3/4

또한 작은 DiT 모델도 오래 학습했다 할지라도 상대적으로 큰 DiT 모델에 비해 compute-inefficient 해짐을 확인하였고 (왼쪽), 작은 모델에서 sampling step을 더 많이 해도 성능 개선과는 연관이 없음을 확인했다 (오른쪽). 가령 오른쪽 그림에서 DiT-L/2 sampling 1000번과 DiT-XL/2 sampling 128번은 FID score가 각각 25.9, 23.7로, 여전히 높게 나옴을 확인할 수 있다.

Reference

Websites

[사이트 출처 1] https://github.com/facebookresearch/DiT/tree/main

Papers

[1] Peebles, W., & Xie, S. (2022). Scalable diffusion models with transformers. arXiv preprint arXiv:2212.09748.

[2] Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., … & Houlsby, N. (2020). An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929.

[3] Zhang, Z., & Schomaker, L. (2022). Divergan: An efficient and effective single-stage framework for diverse text-to-image generation. Neurocomputing, 473, 182-198.

댓글남기기

참고

[Review] Diffusion Models 2 - 작성 중

Diffusion Model이 sample quality 측면에 있어서 높은 fidelity를 자랑한다면, density estimation은 어떨까? log-likelihood를 최소화하도록 Diffusion Model에 약간의 변형을 줘 본, 아래 2개의 논문을 리뷰해보자.

[Review] Diffusion Models 4 - 작성 중

Diffusion Model의 Reverse sampling을 더 빠르게 하는 새로운 방식으로 Distillation Approach가 제안되었다. 아래 2가지 논문을 살펴보자.

[Review] Diffusion Models 3 - 작성 중

Song et al., 2020의 Score-Based Generative Modeling through Stochastic Differential Equations 논문에서 우리는 Diffusion forward process가 forward SDE로 나타나고, reverse p...

[Review] PEFT-LoRA

Parameter Efficient Fine-Tuning(PEFT)라 불리는 모델 튜닝 방식에 대해서, 그 중에서도 Alpaca에서도 사용되는 등 가장 널리 알려진 Low-Rank Adaptation of LLM(LoRA)에 대해 정리해보자.