[Review] Transformer

ChatGPT에게 자신의 부모(?)인 Transformer 모델에 대해 설명을 요청한 결과, 내용을 굉장히 잘 정리해서 알려주고 있다!

“Transformer 모델은 자연어 처리 분야에서 최근에 개발된 딥러닝 모델 중 하나로, 특히 기계 번역, 자연어 이해, 질의응답 등 다양한 자연어 처리 태스크에서 높은 성능을 보이며 널리 사용되고 있습니다. Transformer 모델은 기존의 RNN(Recurrent Neural Network)이나 CNN(Convolutional Neural Network)과는 달리, 어떠한 시퀀스 정보도 전달하지 않으면서 장기 의존성(Long-term dependency) 문제를 해결할 수 있는 모델입니다. 이를 가능하게 하는 것은 Self-Attention(자기 주의) 메커니즘입니다.

Self-Attention은 입력 시퀀스의 각 단어들이 서로 어떤 관련이 있는지를 파악하여, 높은 상관관계를 가진 단어들을 더 중요하게 취급하고, 이를 통해 입력 시퀀스 전체를 동시에 처리할 수 있습니다. 이를 통해 Transformer 모델은 장기 의존성을 포함한 매우 긴 시퀀스에서도 높은 성능을 발휘할 수 있습니다. 또한 Transformer 모델은 인코더-디코더(Encoder-Decoder) 구조를 사용하여 기계 번역, 질의응답 등의 태스크를 수행합니다. 인코더는 입력 문장을 벡터 형태로 변환하고, 디코더는 이 벡터를 바탕으로 출력 문장을 생성합니다. 이 때, 인코더와 디코더는 각각 여러 층으로 구성되어 있으며, 각 층은 여러 개의 Self-Attention과 Feed-Forward 네트워크를 포함합니다.

Transformer 모델은 이러한 구조와 Self-Attention 메커니즘을 통해 자연어 처리 분야에서 높은 성능을 보이고 있으며, 이를 기반으로 한 BERT, GPT 등의 다양한 변형 모델들이 개발되어 사용되고 있습니다.”

“Attention Is All You Need(Vaswani et al., 2017)^[1] 논문을 직접 읽어보면서 자세한 사항들을 알아보자.

1. Introduction

Existing Model

LSTM (Long Short-Term Memory)^[2]

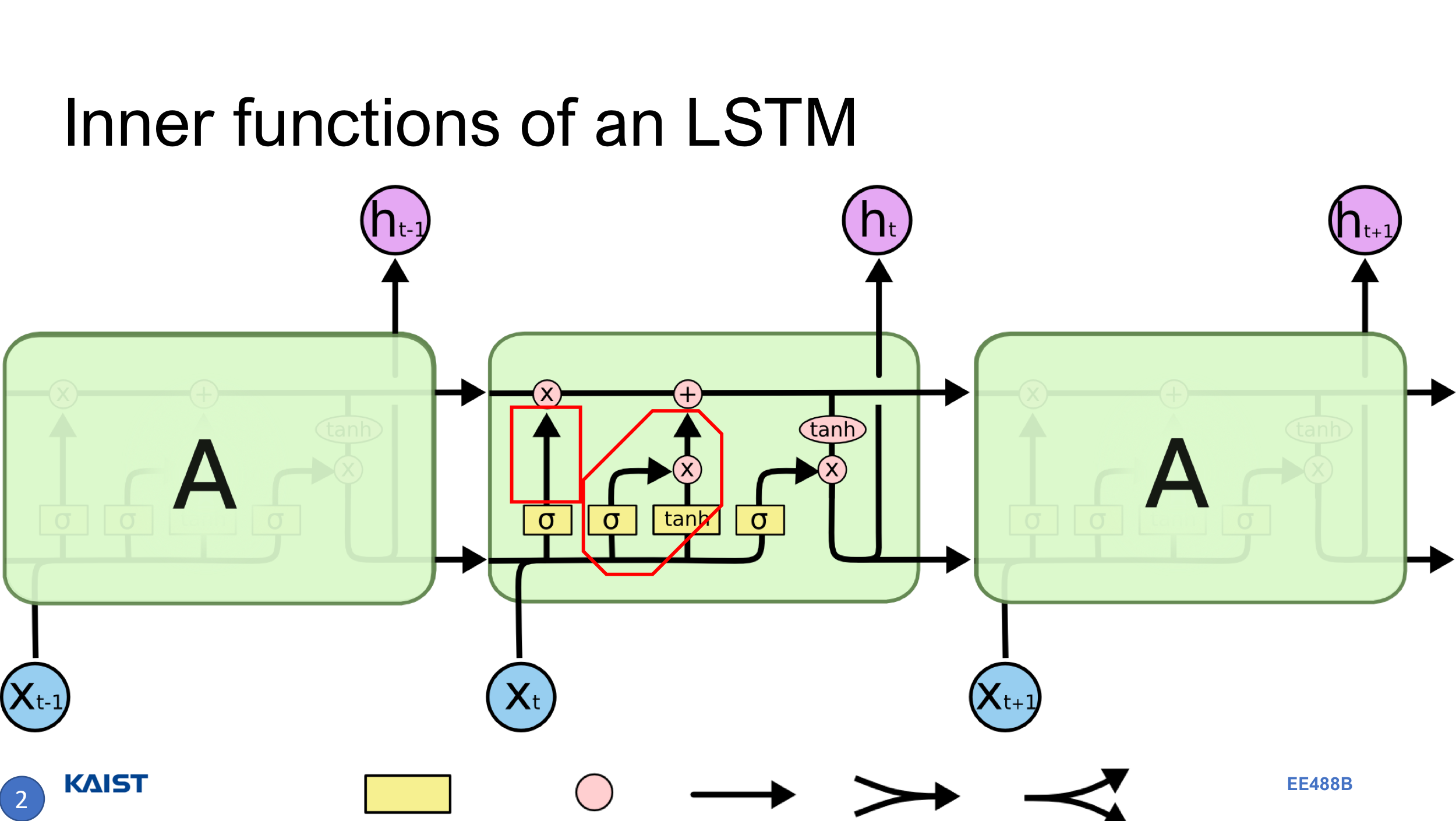
Speech나 Video와 같은 데이터를 처리함에 있어서 기존에는 주로 RNN을 사용하였다.

\[\left\{\begin{matrix} h^{(t)}=f(h^{(t-1)},x^{(t)}) \\ y^{(t)}=g(h^{(t)}) \end{matrix}\right.\]

식에서도 알 수 있듯이, RNN은 $t$에서의 ouput을 결정하는 hidden state $h^{t}$가 이전 layer의 hidden state $h^{t-1}$에만 의존한다. (물론 input도 있긴 하지만) 그래서 Layer가 길어질 수록 old observation은 forgotten되는 문제점이 있다. 추가적으로 SGD가 매우 noisy해져서 vanishing gradient 문제, 혹은 gradient가 explode 될 수 있다.

LSTM은 RNN의 장기의존성(Long-range dependency)를 개선한 모델로, “과거의 기억을 까먹는 것 또한 학습해야 된다”라고 이해하면 좋다. 그림에서 볼 수 있듯이, 하나의 모듈에 3개의 Gate를 거치게 된다. 가장 핵심적인 부분은 Cell state로, 그림에서 가장 위 쪽, $C_{t-1}$에서 $C_{t}$로 이어지는 수평선에 해당한다.

첫 번째 Gate(Forget Gate)는 sigmoid와 pointwise-multiplication으로 이루어진, “Cell state로부터 어떤 정보를 버릴래?”에 대한 것을 결정한다. sigmoid 값이 0 근방이라면 forget, 1 근방이라면 remember가 된다.

두 번째 Gate(Input Gate)는 sigmoid와 tanh의 mulitplication을 더하는, “Cell state에 어떤 정보를 더할래?”에 대한 것을 결정한다. sigmoid를 거친 값은 “어떤 indices를 쓸래?”, tanh를 거친 값은 “해당 indices에 뭘 쓸래?”로 해석할 수 있다. multiplication으로 인해 해당이 붙었다 생각하면 되고, 이것이 Cell state에 더해지게 된다. 더해지는 과정을, “앞에서 정보를 버렸으니, 이번엔 선택된 정보를 써보자”로 이해할 수 있겠다.

마지막 Gate는 sigmoid와, tanh를 거친 Cell state의 multiplication으로 이루어진, “최종 output으로 뭘 할래?”에 대한 것을 결정한다.

GRU (Gated Recurrent Unit)^[3]

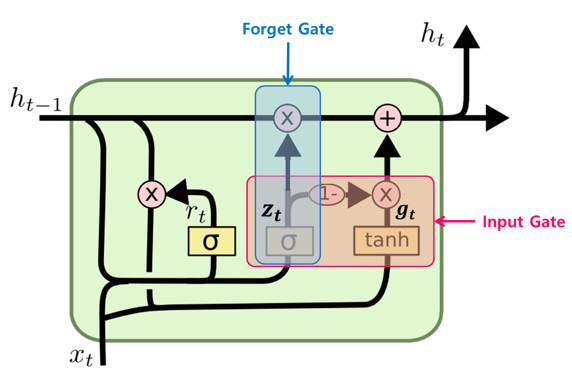
한국인의 논문이라니

Transformer 논문에서 소개된, LSTM의 변형 작 중 하나이다. 자세히 읽어보지는 않았지만, 그림만 봤을 때는 Cell state가 hidden state와 합쳐져있고, Forget gate와 Input gate가 합쳐진 변형 모델과 비슷한 듯 다르며, 또 여러가지 변경 및 개선사항이 있는 것 같다. 결과적으로 기존 LSTM보다 단순한 구조(그림만 보면 단순해 보이지는 않지만)를 가져서 인기가 있다고 한다.

Encoder-Decoder

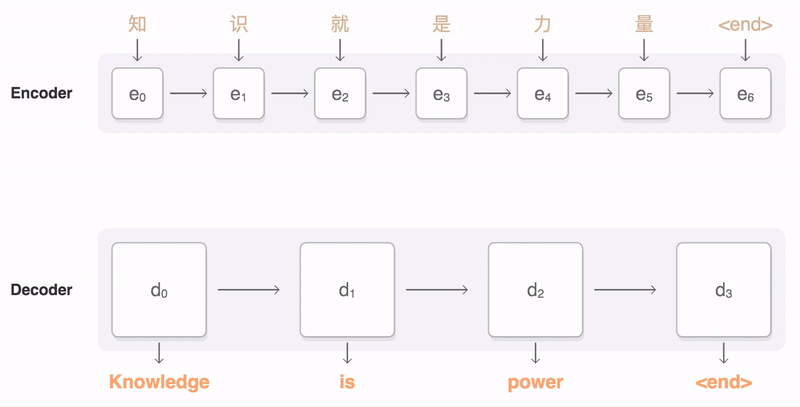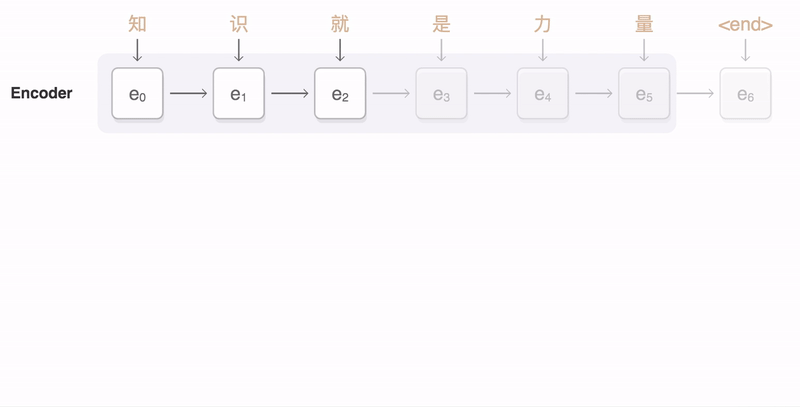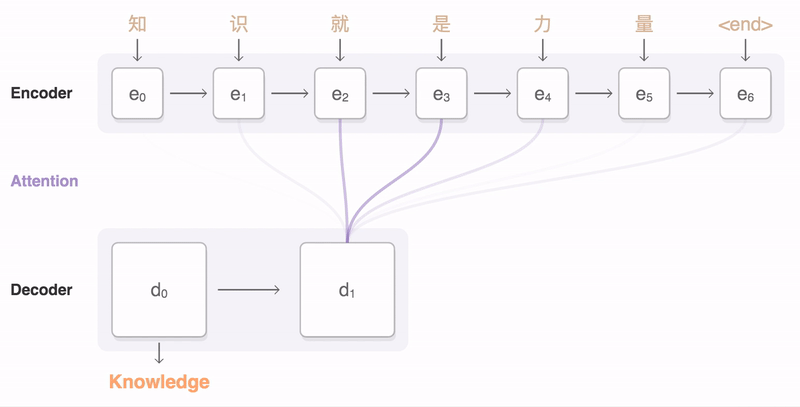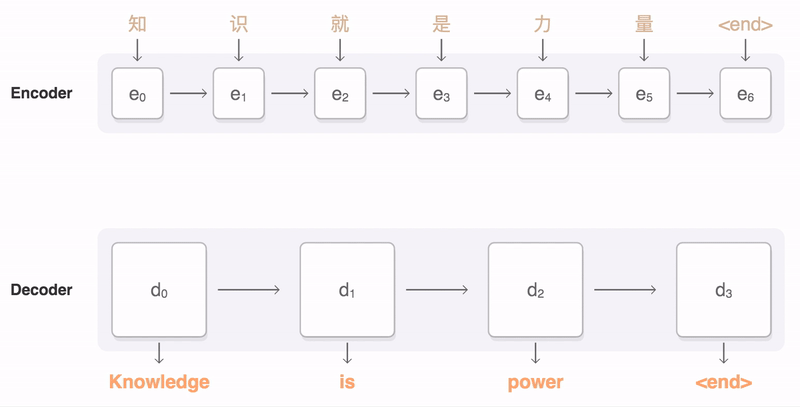
Seq2seq 모델은 Encoder를 통해 input을 Context vector로 표현하고, Decoder를 통해 Context vector를 output으로 변환하는 구조이다. 이 때 Context vector의 크기가 고정되어 있어, input이 길 경우 성능이 좋지 않아지게 되는데… 이를 개선하는 법이 그림에도 나와있는, 그리고 Transformer 논문에서도 중요 사항이 되는 Attention Mechanism이다.

위 문제점을 개선하기 위해서 고안한 아이디어는 “hidden state들 중에서, 현재 $t$에서의 ouput을 결정하는 가장 중요한 hidden state는 무엇일까?”이다.

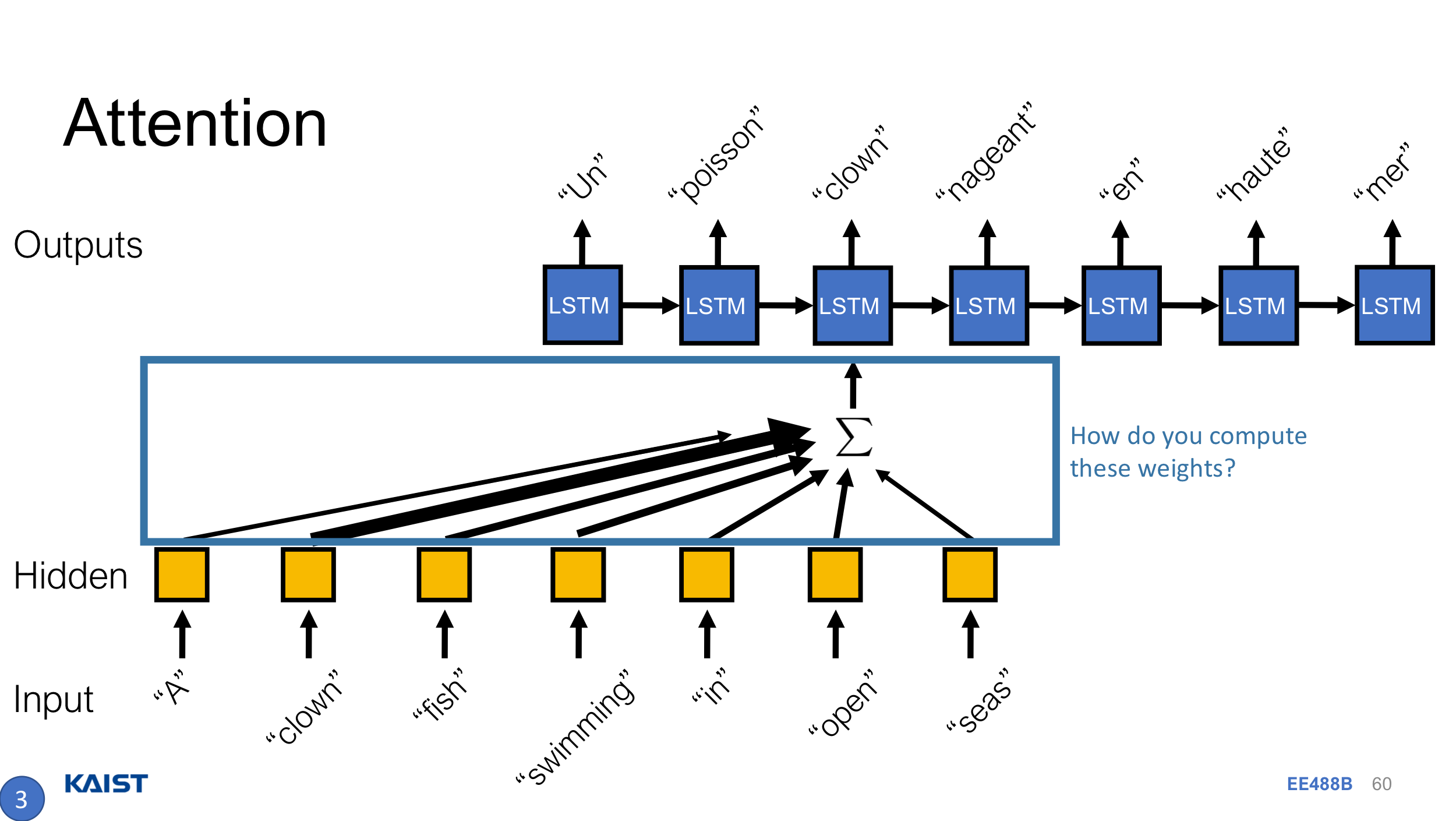
결국 그림에서의 attention weight를 구해서, context vector를 hidden vector의 weighted sum으로 표현하게 된다. 여기서 attention weight를 구하는 방법은 여러가지가 제안되어 있었는데, 대표적인 건 Bahdanau^[4] 씨의 식과 Luong 씨의 식이 있는 것 같다만 자세히 살펴보지는 않겠다.

논문에서도 위의 모델이 sequence modeling과 transduction problem에서 SOTA임을 말하며 간단히 소개하고 있고, 자신들의 모델인 Transformer는 Recurrence를 회피(eschew)하고 attention mechanism에 entirely 의존하여 global dependency를 이끌었다고 말하고 있다. Attention을 RNN/LSTM과 함께 활용한 모델이 대부분이라, Transformer는 이에 벗어나서 이제 sequential data를 병렬화(Parallelization) 처리할 수 있게 된 것이다.

“The Transformer allows for significantly more parallelization and can reach a new state of the art in translation quality after being trained for as little as twelve hours on eight P100 GPUs.”

2. Background

바로 위에서 말한, sequential data를 병렬처리하는 것과 관련하여 한 번 더 얘기를 하고 있다. Transformer 이전에도 당연히 sequential computation cost를 줄이기 위해 여러 노력들을 했는데, 논문에서 소개한 것은 Extended Neural GPU (Kaiser et al., 2016), ByteNet (Kalchbrenner et al., 2017), 그리고 ConvS2S (Gehring et al., 2017)이다. 3가지 모델 모두 CNN을 기반으로 sequential data에서 hidden representation을 계산하는데, 두 개의 임의의 input 또는 output position에서 신호를 연관짓는데 operation 수가 position간 거리에 대해 ConvS2S는 linear하게, ByteNet은 logarithmic하게 증가한다고 한다. (해당 모델들을 자세히 본 적이 없어서 모름) 이는 멀리 떨어진 position간의 의존성을 학습하기에 부적합한 사항인데, Transformer에서는 operation 수가 constant여서 효과적이다고 말하고 있다! (그 이유가 Multi-Head Attention이라는데, 이는 3-2 Attention에서 다뤄보자.)

Self-attention은 논문에서도 자세히 설명하지만, 간단하게 정리하고 밑에서 또 알아보자. 3-2

우선 위에서 봤던 seq2seq 모델에서의 attention 메커니즘을 Query, Key, Value로 조금 더 일반화 해보자. 주어진 Query에 대해 모든 Key와 유사도를 구하고, 이를 가중치로 표현하여 각각의 Value에 반영해준다. 그래서 이 Value를 다시 weighted-sum하여 최종적으로 Query를 리턴하게 된다.정리하자면, Query Q:어떤 시점 $t$에서 Decoder의 hidden state, Key K:모든 시점에서 Encoder의 hidden state, Value V:모든 시점에서 Encoder의 hidden state가 되겠다. 여기서 봐야할 점은 Q가 K,V와 출처가 다르다(값이 다르다)는 점.

그렇다면 Self-attention은 말 그대로 Q가 K,V와 출처가 같은(값이 같은) 메커니즘으로, 예를 들면 Q,K,V 모두 입력한 문장의 단어 vector들(혹은 이들의 hidden state)로 생각할 수 있겠다. 이 짓을 왜 할까? 아주 잘 설명하는 그림 및 문장이 있다.

영어 문장에서 대명사 it, 한글로 치면 ‘그것’, ‘저것’ 할 때 진짜 ‘그것’이 의미하는게 무엇인가를 학습하는 데에 self-attention이 좋은 방법이 될 수 있다. 그림에서 it이 animal인지, street인지 우리는 쉽게 알지만 기계는 모르기 때문에 self-attention으로부터 animal임을 학습하는 것을 보여주고 있다.

End-to-end memory network는 말 그대로 end-to-end로 학습된, Memory Network이다. Memory network는, encoder-decoder 구조에서 context vector가 입력이 매우 길 때 입력의 앞부분을 반영하기 힘든 문제를 해결하기 위해 제안된 것으로, 메모리에 저장할 수 있는 만큼 최대한 각 단계에서 hidden state를 저장해 써 먹는 것이다.

아무튼, Transformer는 sequence-aligned RNN이나 Conv를 쓰지 않고, input의 representation을 오직 self-attention mechanism에만 의존하는 최초의 변환 모델이다.

이제 본격적으로 Transformer의 구조를 자세히 알아보자!

3. Model Architecture

기본적인 구조는 seq2seq의 encoder-decoder structure를 따라간다. 차이라면 seq2seq는 Encoder가 모두 처리된 이후에 Decoder 연산이 시작될 수 있지만, Transformer는 동시에 된다는 점 정도.

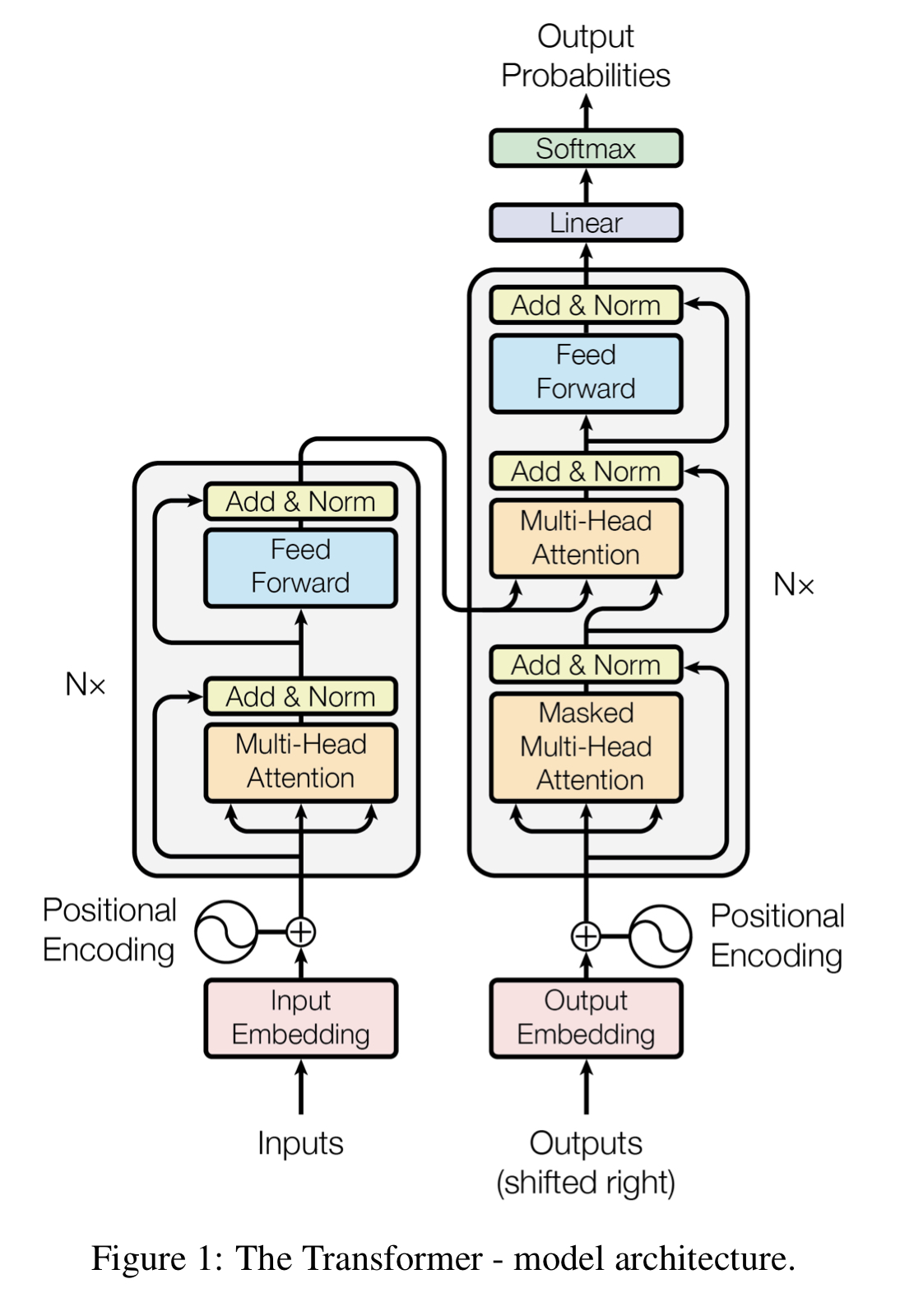
3-1. Encoder and Decoder Stacks

Fig. 1의 왼쪽에 해당하는 Encoder는 총 $N=6$개의 동일한 layer를 쌓았다. (마지막 6번째 Encoder layer의 결과가 Decoder에게 전달되겠다) 각 layer는 2개의 sub-layer로 구성되어 있는데, 첫 번째는 multi-head self-attention layer, 두 번째는 position-wise fully-connected feed-forward layer이다. 각각의 sub-layer 모두 네트워크를 거친 뒤 residual connection&Norm을 해주고 있다. 이 때의 Norm은 LayerNorm. BatchNorm은 하나의 채널 방향으로 normalize 하는거라면, LayerNorm은 하나의 batch 방향으로 normalize 하는 거다. 아래 사진은 다양한 Normalizion을 그림으로 잘 보여주고 있다. ^[5](N:# of minibatch, C:# of channel, H,W:height, width)

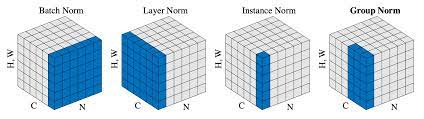
아무튼, $LayerNorm(x+Sublayer(x))$로 각 sub-layer에서 output을 도출한다.

Fig. 1의 오른쪽에 해당하는 Decoder는 Encoder와 동일하게 총 $N=6$개의 동일한 layer를 쌓았다. Encoder의 두 가지 sub-layer를 동일하게 쌓고, 추가적으로 중앙에 multi-head attention (self-attention이 아니다! 마지막 Encoder의 output을 attention input으로 넣고 있다.)을 수행하는 3 번째 sub-layer를 추가해주었다. 또한 self-attention layer를 masking 해서 살짝 수정해주었는데, 이를 통해서 현재 시점의 예측에서 현재 시점보다 미래에 있는 단어들을 참고하지 못하도록 해준다.

Encoder와 Decoder의 입출력 크기 및 embedding layer의 차원은 $d_{model}=512$로 고정해두었다.

3-2. Attention

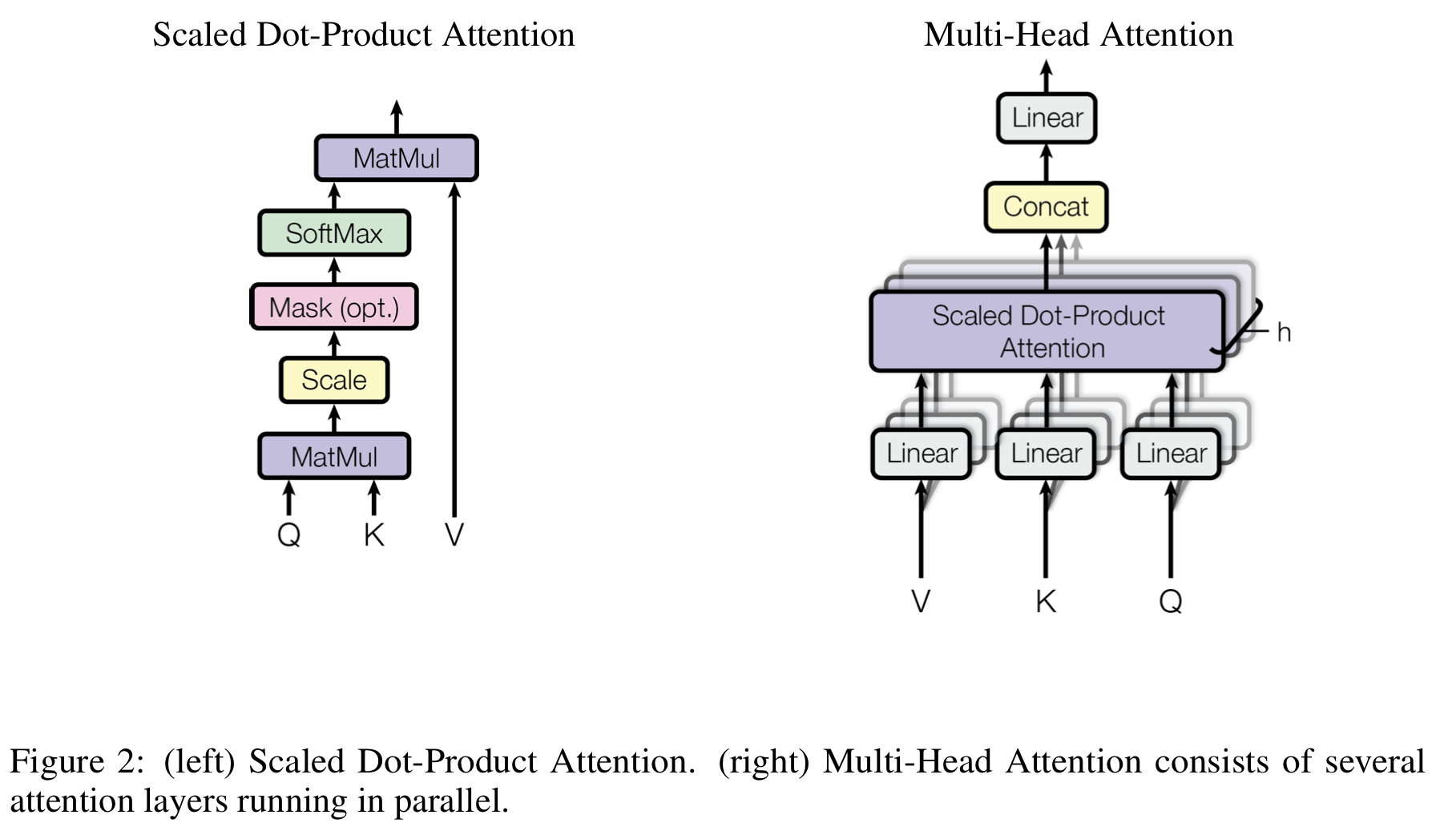
3-2-1. Scaled Dot-Product Attention

Query Q와 Key K의 차원을 $d_{k}$, Value V의 차원을 $d_{v}$라고 할 때, 1. Q와 K dot product / 2. $\sqrt{d_{k}}$로 divide / 3. Softmax를 수행하는 Attention mechanism이다.

\[Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V\]

Fig 2. 왼쪽 그림에 나타나있고, 말 그대로 Dot-product를 수행하고 scaling을 진행하는 걸 볼 수 있다.

Attention mechanism으로 additive attention이 아닌 dot-product attention을 채택함으로써 매우 최적화된 행렬곱 연산을 사용할 수 있기에 학습에서 속도가 매우 빨라졌다. 또한, Q, K의 차원 $d_{k}$가 매우 크다면 dot product를 하는 과정에서 값이 매우 커지고, softmax를 거치기에 vanishing gradient 문제를 이끌 수 있기에, scaling 과정을 거쳐 이를 해결할 수 있는 장점이 있다.

Padding Mask

잠깐 Pytorch의 torch.nn.TransformerEncoder의 forward 함수를 보자.

forward(src, mask=None, src_key_padding_mask=None)

함수 인자로 $(S,N,E)$ shape의 src, $(S,S)$ shape의 mask, $(N,S)$ shape의 src_key_padding_mask를 받고 있다. src는 encoder에 들어올 sequence라 필수이고, 나머지 2개가 있는데. src sequence에 masking 하는지, src의 key K에 masking 하는지 그 차이다. 자세한 내용은 아래에서 다뤄보자. Pytorch Transformer

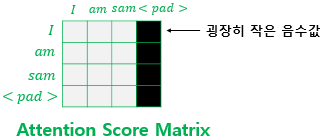
그림과 같이, 어떤 입력을 받을 때 입력의 길이가 일반적으로는 다르기에 뒤에 padding이 붙어져 있는 경우가 있다. 이 때 attention을 수행하면 별 문제가 생기는 건 아니고 결과를 출력하기는 할 텐데, 사실 padding은 의미가 없기에 softmax를 거쳤을 때 그림에서 오른쪽에 pad가 있는 행과 열은 0 값이 되면 좋다. 그래서 고의적으로 -1e9 같은 큰 음수를 넣어서 output을 0으로 만들고 pad 토큰은 반영되지 않도록 하는 것이다.

3-2-2. Multi-Head Attention

$d_{model}=512$차원의 Q,K,V에 1개의 attention function을 적용해도 별 문제는 없지만, 논문 저자는 여러번의 attention을 병렬로 처리하는 것이 더 beneficial하다고 말하고 있다. 여기서 말하는 beneficial은 성능이 좋다기 보단 속도가 빨라져서 효과적이라는 것 같다. 그래서 Q,K를 $d_{k}$차원, V를 $d_{v}$차원으로 ($d_{k}=d_{v}=d_{model}/h=64$) linear projection하여 총 $h=8$개의 parallel attention layer를 수행하고, 이들을 다시 concat하여 linear layer에 보낸다.

\[MultiHead(Q,K,V)=Concat(head_{1},...,head_{h})W^{O} \\ where \; head_{i}=Attention(QW_{i}^Q,KW_{i}^K,VW_{i}^V)\]

$W_{i}^Q \in \mathbb{R}^{d_{model} \times d_{k}},W_{i}^K \in \mathbb{R}^{d_{model} \times d_{k}},W_{i}^V \in \mathbb{R}^{d_{model} \times d_{v}},W^{O}\in \mathbb{R}^{d_{model} \times hd_{v}}$

Look-ahead Mask

Decoder에서 Encoder와 다르게, self-attention sub-layer에 masking을 해준다.

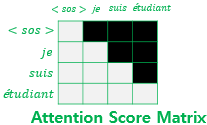
그림에서 각 행을 보면 자기 자신과 그 이전 단어들에만 결과가 의존하게 된다. 이는 auto-regressive property, 시간 $t$에서의 output은 이전 $t-1,…$에만 의존하는 일종의 causality를 수행하는 것이다.

3-2-3. Applications of Attention in our Model

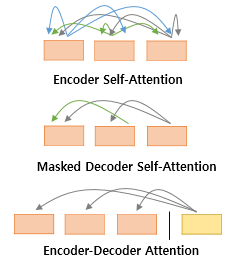
정리하자면, Transformer는 multi-head attention을 3가지 다른 방식으로 쓰고 있는데,

1. “Encoder-decoder attention” Layer에서는 K, V가 encoder의 ouput 값이고 Q는 이전 decoder의 값을 쓴다. 앞서 한 번 말했지만 self attention이 아니며, seq2seq 모델의 encoder-decoder attention 구조와 유사하다고 보면 된다.
2. Encoder의 self-attention Layer에서는 K, V, Q 모두 이전 encoder의 값을 쓴다.
3. Decoder의 self-attention Layer에서도 K, V, Q 모두 이전 decoder의 값을 쓰지만, Masking을 해준다. Look-ahead Mask 앞서 말했듯이 auto-regressive property를 preserve 해준다.

3-3. Position-wise Feed-Forward Networks

Multi-Head Attention layer를 살펴보았으니 이제는 또 다른 sub-layer인 Feed-Forward Fully-connected layer를 살펴보자. 여러개의 layer를 쌓아도 되지만, 논문에서는 2개의 층을 쌓았고, activation은 당연히 ReLU를 썼다. 즉, $FFN(x)=ReLU(xW_{1}+b_{1})W_{2}+b_{2}$. Input과 output은 앞서 고정해둔 차원 $d_{model}=512$이고, 2개의 층 사이의 hidden state는 차원 $d_{ff}=2048$로 설정해두었다.

3-4. Embeddings and Softmax

최종적으로는 Decoder의 최종 output에서, linear layer와 softmax를 통해 다음 token을 예측하는 확률을 뽑게 된다. 이 때, pre-softmax linear transformation의 weight와 two embedding layers의 weight를 sharing 하는데, Fig 1. 전체 구조에서 Input과 Target을 우리는 embedding layer를 통해 $d_{model}$ 차원으로 보내주었었다. 이 weight를 공유하는 것 같다. linear transformation을 거치기 직전 값이 구조적으로 input의 embedding과 비슷한 놈으로 취급할 수 있을테니, 이 짓을 하는 것 같다.

3-5. Positional Encoding

Transformer 모델은 recurrence나 convolution을 전혀 쓰지 않기 때문에, sequence의 순서 정보를 포함하기 위해서 “positional encodings”라는 것을 input embedding에 더해준다. 그림에서 embedding과 position 정보를 sum하고 있으니, 당연히 차원은 $d_{model}$로 맞추어 준다. 논문에서 사용한 positional encoding은 다음과 같다.

\[PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}}) / PE_{(pos,2i)}=cos(pos/10000^{2i/d_{model}})\]

pos는 position, i는 dimension을 뜻해서 positional encoding의 각 dimension이 sinusoid에 해당하게 한다. 위 식으로 정한 이유는 모델이 상대적인 position을 학습함에 있어서 $PE_{pos+k}$가 $PE_{pos}$에 대해 linear 하기 때문에 쉽게 학습할 것이라 추측하고 있기 때문이라고 한다. 굉장히 합리적으로 보이긴 한다. 또한 sin, cos 두 개가 거의 동일한 결과를 보인다고 한다.

최근에는 이런 방식 보다는 torch.nn.Embedding(num_embeddings, embedding_dim)과 같은 embedding 방식을 채택하고 있다고 한다. torch의 transformer도 이거 써서 했다.

3-6. Summary

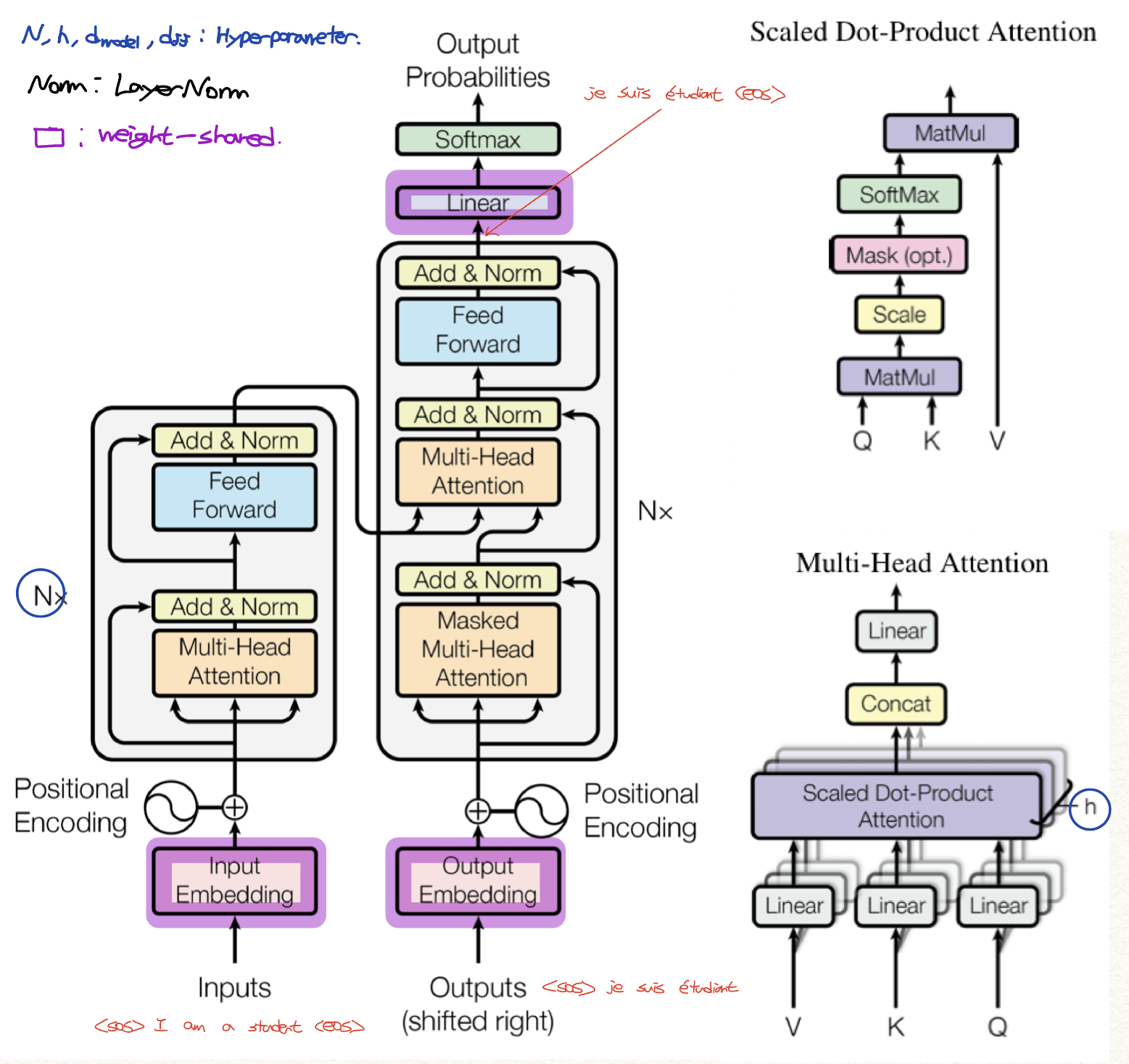
Hyperparameters

1. $N_{E}(=6)$, $N_{D}(=6)$: Encoder Layer와 Decoder Layer 개수
2. $d_{model}(=512)$: Encoder/Decoder input과 output의 차원
3. $h(=8)$: Multi-head Attention에서 attention layer 개수
4. $d_{ff}(=2048)$: FC Layer에서 hidden feature 차원

Encoder

우선 Embedding Layer를 거친 input과 Positional Encoding을 한 input을 더해 첫 번째 encoder의 input으로 사용한다. Encoder는 Multi-Head self-attention layer를 거쳐 FC Layer를 거치게 된다. 각 layer마다 Residual connection & LayerNorm을 수행하며, 마지막 encoder를 거친 결과는 Decoder로 향하게 된다.

Decoder

Linear-Softmax를 거치기 이전의 Output(그림 상 위쪽의 output)을 다시 Decoder의 input(그림 상 아래쪽의 outputs(shifted right))로 넣어준다. Right-shifted된 Output을 Embedding Layer를 거친 것과 Positional encoding한 것을 더해서 첫 번째 decoder의 input으로 사용한다. Decoder는 Masking Multi-Head self-attention layer를 추가해 미래의 output에 영향을 받지 않도록 하고, Encoder의 결과를 K,V로 한 Multi-head attention layer를 거친 뒤 FC layer를 거치게 된다. 끝으로, FC-Softmax를 통해 다음 토큰의 output을 예측하는데, 이 때 Linear는 embedding layer와 weight-share 되어 있다.

torch.nn.Transformer

Pytorch Transformer

torch.nn.Transformer(d_model=512, nhead=8, num_encoder_layers=6, num_decoder_layers=6, dim_feedforward=2048, dropout=0.1, activation=, custom_encoder=None, custom_decoder=None, layer_norm_eps=1e-05, batch_first=False, norm_first=False, device=None, dtype=None)

parameter로는, Transformer model의 hyperparameter인 d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward, dropout. 그리고 activation을 gelu로 바꾸거나 customizing한 encoder, decoder를 쓸 수도 있다. 눈 여겨 봐야 될 점은 batch_first. 학습을 할 때 Default로 들어가는 shape은 (seq, batch, feature)로 (batch, seq, feature) shape의 데이터를 쓰기 위해서는 batch_first=True로 설정해주어야 된다.

forward는 다음과 같이 되어 있다.

forward(src, tgt, src_mask=None, tgt_mask=None, memory_mask=None, src_key_padding_mask=None, tgt_key_padding_mask=None, memory_key_padding_mask=None)

src는 encoder input, tgt는 decoder input (right-shifted output)으로 필수이다. src_mask, tgt_mask, memory_mask, src_key_padding_mask, tgt_key_padding_mask, memory_key_padding_mask는 각각 Encoder의 Multi-head self-attention, Decoder의 masked Multi-head self-attention, Decoder의 Multi-head attention layer에서의 mask 여부다. 여기에 아주 답변이 잘 달려있다:Different type of maskings. 가장 중요하다고 볼 수 있는건 tgt_mask이다. 이것이 바로 auto-regressive property를 보장해 주는 masking이다.

4. Why Self-Attention

self-attention layer가 recurrent나 convolutional layer에 비해 어떤 점이 좋은지 비교하고 있다. 첫 번째는 layer마다 총 computational complexity, 두 번째는 병렬화 될 수 있는 computation 양, 그리고 세 번째는 long-range dependency 정도.

5. Training

여기서 몇 가지 살펴볼 사항으로는,

1. 각 sub-layer의 output을 Residual Sum&Norm 하기 이전에 dropout $P_{drop}=0.1$을 했다는 점
2. Label smoothing $\epsilon_{ls}=0.1$을 썼다는 점

6. Results

여기서 몇 가지 살펴볼 사항으로는,

1. Big model: $N=6,d_{model}=1024,d_{ff}=4096,h=16,d_{k}=d_{v}=64, P_{drop}=0.3$ Hyperparameter로 조금 더 좋은 BLEU(BiLingual Evaluation Understudy) 점수를 뽑아냈다는 점

Reference

Websites

사이트 출처 1 (https://wikidocs.net/31379) 사이트 출처 2 (https://gaussian37.github.io/dl-concept-transformer/) 사이트 출처 3 (https://stackoverflow.com/questions/62170439/difference-between-src-mask-and-src-key-padding-mask)

Images

[그림 출처 1] 2022 Fall EE488(B) DL for CV Lecture Note (by Prof. Jung) 그림 출처 2 (https://excelsior-cjh.tistory.com/185) 그림 출처 3 (https://google.github.io/seq2seq/) 그림 출처 4 (https://gaussian37.github.io/dl-concept-transformer/)

Papers

글에서 나오는 내용 순서대로 참고한 논문이 작성됨

[1] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.

[2] Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.

[3] Chung, J., Gulcehre, C., Cho, K., & Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555.

[4] Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.

[5] Wu, Y., & He, K. (2018). Group normalization. In Proceedings of the European conference on computer vision (ECCV) (pp. 3-19).