[CS231n] Lecture 3&4

February 27, 2023

Lecture 3 - Loss Functions and Optimization

Lecture 2에서 못 다한 이야기, 2가지가 있다.

그래서, 분류를 잘하는 W는 무엇인가?
어떻게 W를 분류를 잘하는 W로 학습할 것인가?

Loss Function

A Loss function tells how good our current classifier is.

Input Dataset이 $(x_{i}, y_{i})^{N}$로 주어질 때, ($x_{i}$는 image data고 $y_{i}$는 label) Loss function이 $L_{i}$로 주어진다면 최종 Loss는 다음과 같이 정의한다: $L=\frac{1}{N}\sum_{i}^{}L_{i}(f(x_{i},W),y_{i})$

Multi-class SVM loss

Support Vector Machine (SVM)을 Multi-class version으로 확장한 Loss. 수식으로는 다음과 같다. $\sum_{j\neq y_{i}}\begin{cases} 0& \text{ if } s_{y_{i}}\geq s_{y_{j}}+1 \\ s_{j}-s_{y_{i}}+1& \text{ if } o.w. \end{cases} =\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+1)$

Multiclass SVM loss를 그래프로 그려보면, $s_j$를 기점으로 margin(여기서는 1)보다 더 클 경우 0, 그 전에는 linear 하게 감소하는 Hinge 모양이 된다. (그래서 Hinge Loss라고도 부른다.)

의미적으로는, ground-truth label의 score 값이, 다른 label의 score 값보다 margin 이상으로 컸으면 좋겠다 는 뜻이다. 식에서도 알 수 있지만, score 값의 절대적인 수치가 중요한 것이 아니라 상대적인 차이가 의미가 있는 것이다.

추가적으로, Loss가 0이 되는 weight W는 unique 하지 않다. (ex: DOUBLE W ~~DOUBLE DOUBLE U=quad U~~)

Softmax loss (Multinomial Logistic Regression)

Softmax Loss 도 Multi-class image classification에서 많이 쓰인다. (특히 딥러닝에서) 수식으로는 다음과 같다.

\[L_{i}=-log(\frac{e^{s_{y_{i}}}}{\sum_{j}^{}e^{s_{j}}})\]

MultiClass SVM Loss와는 다르게, score의 절대적인 수치가 의미가 있게 된다. 왜냐하면, negative log 이전 수치가 class로의 probability로 의미를 가지기 때문이다.

Regularization

“Among competing hypotheses, the simplest is the best” - William of Ockham

모델이 Overfitting하는 경우에 penalty를 부과해주는 값이다 (그림에서 R(W) term. 그림에 Regularization Loss에 가중치를 다르게 부여하는 hyperparameter $\lambda$가 빠져있다.). 지금 Lecture에서는 L2 Regularization (Weight Decay), L1 Regularization, Elastic net(L1, L2 짬뽕)을 알려주고 L-$\infty$ (Max norm) Regularization, Dropout, Batch Normalization, stochastic depth 등은 나중에 알려줄 예정인갑다.

3_1

Optimization

1번 질문에 대한 대답은 끝났다: Loss 값이 가장 적은 W를 채택할거다! 그렇다면 이제 2번 질문에 대한 대답을 할 차례이다: 어떻게 W를 학습할 건가. ~~Random search로 W 찾기 같은 짓거리는 하지 않는다~~

Gradient Descent (GD)

Vector-variable Calculus에서 했듯이, negative gradient가 steepest descent direction인 점을 이용하여 weight W를 update 한다. 아래 그림에서 처럼 Loss(Error)가 가장 적은 W를 향해 나아가는 것이다. Numerical하게 Weight 값을 아주 조금 증가시켰을 때 Loss의 변화를 관찰해도 되지만, Analytic하게 $\frac{\partial L}{\partial w_{ij}}$ 식을 특정하고 값을 구하는게 더 좋다.

3_2

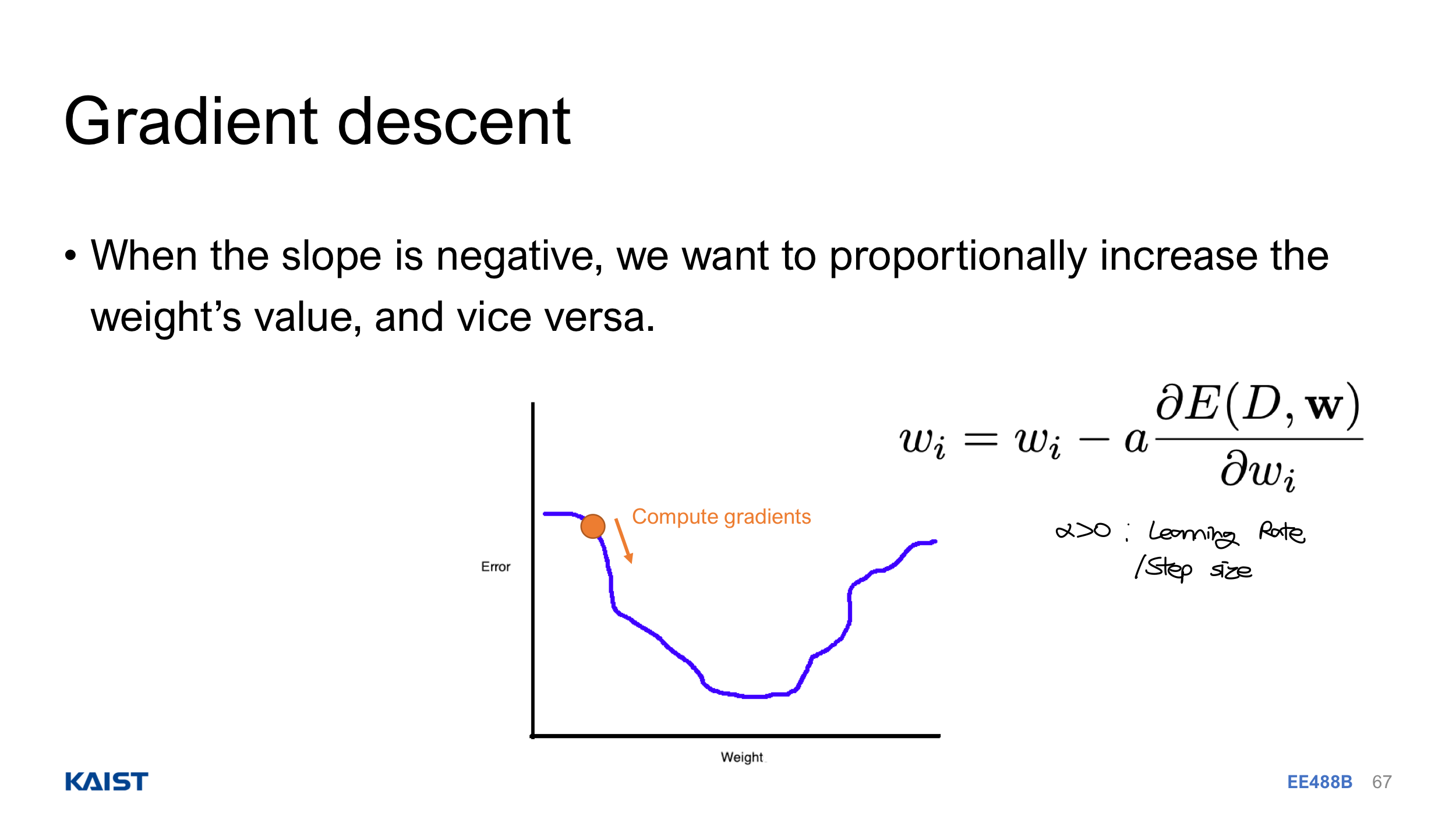
Pseudo-Code로는,

    while True: # 적당할 때 멈춰야 겠죠?
        weights_grad = evaluate_gradient(loss_func, data, weights)
        weights += - learning_rate * weights_grad # Parameter Update

위에서 언급한 Regularization Penalty term이 추가되어도, Derivative는 Linear Operator이기에 별로 복잡한 게 없다. ~~역시 Linear이 최고~~

Stocastic Gradient Descent (SGD)

위 코드에서 만약에 Data가 Imagenet 같이 1 million을 넘어가면, gradient를 계산할 때 마다 백만 개의 데이터를 참조해야 되고, 계산이 too expensive 해진다. 따라서, minibatch (typically 2의 n승) data만 참고하여 gradient를 구하고 업데이트 하는 방법을 채택한다.

Pseudo-Code로는,

    while True: # 적당할 때 멈춰야 겠죠?
        batch_data = sample_training_data(data, batch_size=2**5)
        weights_grad = evaluate_gradient(loss_func, batch_data, weights)
        weights += - learning_rate * weights_grad # Parameter Update

마지막으로, Hyperparameter인 learning rate는 전체 딥러닝 학습 과정에서 가장 중요한 hyperparameter라 볼 수 있다. 정해진 Rule이 없는 것 같지만, 뭐 이리저리 해보는게 최선..

그리고 Momentum term과, Adam 등 Optimizer&Scheduler에 대한 얘기도 잠깐 언급하고 넘어갔다. ~~이후 Lecture에 나오겠지…~~

Feature Extraction

앞으로의 DL model에서 얘기할 내용을 잠깐 하는거 같은데, Image로부터 feature를 추출하고 이 특징들을 이용하여 image classificaion 같은 task를 한다는 얘기를 하고 있다. Color Histogram, Histogram of Oriented Gradients (HoG), Bag of Words (NLP로부터) 등의 방법으로 feature를 추출하고 classifier model을 학습하는 것이다.

과거에는 이렇게 feature extracter는 학습하는 것이 아니고 어떤 정해진 방법을 사용했지만, 이제는 Deep learning을 통해서 feature extractor도 model의 일부로 보면서 학습하여 parameter를 업데이트 하는 것임을 설명하고 있다.

Lecture 4 - Introduction to Neural Networks

Lecture 3에서 우리는 weights += - learning_rate * weights_grad 방식으로 최적의 weight를 학습한다고 배웠다. 그렇다면 weights_grad를 구하는 방법에 대해 얘기를 해야된다.

BackPropagation

기본적으로

Computational Graph를 떠올려 model 구조를 표현하고,
Intermediate value들을 계산하기 위해 Forward Pass를 거친 뒤,
BackPropagation을 거쳐 gradient를 구한다.

(Maybe Lecture 6 또는 7에서 training network 하면서 다루겠지만) 저 위 과정을 Forward-Backward API로 나타내보자면..

4_1

무튼 최종 Loss 값으로부터 처음 weight의 element 까지 거꾸로 진행해서 BackPropagation인데, Chain Rule만 열심히 쓰면 된다. Jacobian, Gradient matrix size만 check하면서…

BackProp.은 강의에서도 그냥 예시들로 설명하고 있다. 예시 없이는 설명하기 참 힘드니까 그런거 아닐까? 그냥 내가 공부했던 예시 그림으로 넘어가겠다. Loss는 Mean Square Error(MSE), activation으로는 ReLU를 사용한 2-layer NN이다.

4_2

Nerual Networks

지금까지 봤던 model은 linear function, $f=Wx$이다. 우린 굳이 linear function 하나만 할 필요는 없으니까? ~~멍청하게 linear function 여러개 하지 말고.. 그건 계속 one linear layer다~~

$f=W_{2}max(0,W_{1}x)$로 층을 2개, 혹은 $f=W_{3}ReLU(W_{2}\sigma(W_{1}x))$처럼 층을 3개 쌓는 등 여러 층을 쌓으면 된다. Nonlinear Activation Function과 함께!

우리 뇌의 신경망 구조와 동일해서 저런 이름이 붙었다. Lecture Note가 이를 잘 표현해놓고 있다. ~~근데 axon, dendrite, presynaptic terminal 뭐 이런 것들 예전 고등학교 때 한 거 같은데 다 까먹었네~~

4_3

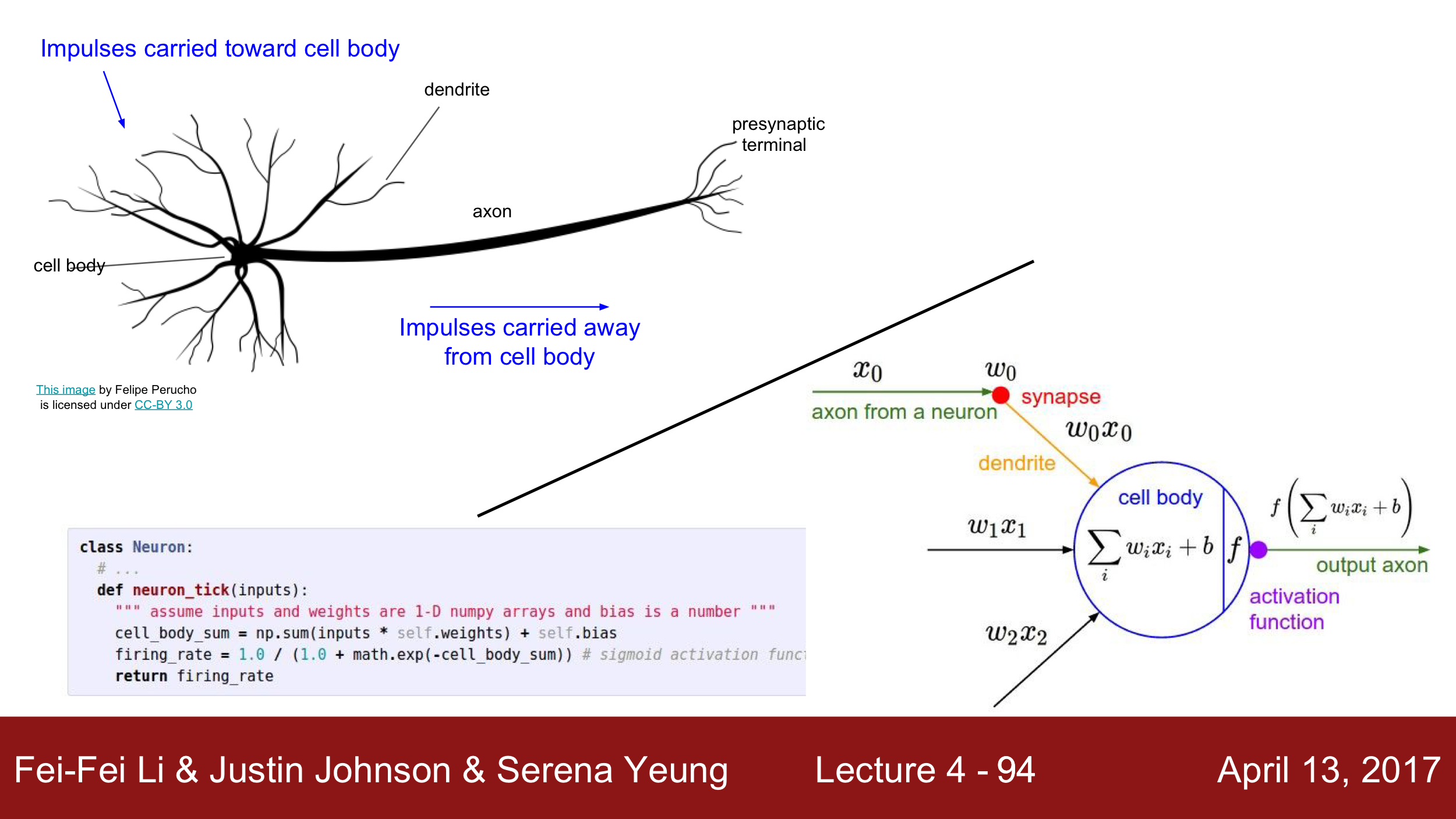
Activation Functions

층을 여러개 쌓기 위한 Nonlinearity, Activation function에 대한 소개를 간단히 하고 있다. Sigmoid, tanh, max, ReLU, Leaky ReLU, ELU 등이 Lecture Note에 있는데, 이후 강의에서 자세히 다룰 예정이라고 하니 그 때 되서 설명을 적는 걸로. 장단점들에 대한 얘기를 하겠지? 아무튼 지금은 Pass.

NN example

2-layer NN에서 Forward-Backward API를 pytorch 버전으로 해보자면?

    import torch
    N, D_in, H, D_out = 64, 1000, 100, 10
    x = torch.randn(N, D_in) # Input
    y = torch.randn(N, D_out) # Label
    # Weight Initialization
    w1 = torch.randn(D_in, H)
    w2 = torch.randn(H, D_out)
    lr = 1e-6
    for t in range(500):
        # Forward Pass
        h = x.mm(w1)
        h_relu = h.clamp(min=0) # ReLU
        y_pred = h_relu.mm(w2) # Output(Prediction)
        loss = (y_pred-y).pow(2).sum() # Loss - MSE
        # BackPropagation. Calcaulte Gradient Analytically
        grad_y_pred = 2.0 * (y_pred - y) 
        grad_w2 = h_relu.t().mm(grad_y_pred) # t(): transpose
        grad_h_relu = grad_y_pred.mm(w2.t())
        grad_h = grad_h_relu.clone()
        grad_h[h < 0] = 0
        grad_w1 = x.t().mm(grad_h)
        # Weight update
        w1 -= lr * grad_w1
        w2 -= lr * grad_w2

사실 Pytorch는 우리를 위해 Linear layer는 물론, Forward Pass, Backpropagation 까지 코드 한 줄로 가능케 해준다. 위에 꺼를 최대한 간단하게 해보자면…

    import torch
    N, D_in, H, D_out = 64, 1000, 100, 10
    x = torch.randn(N, D_in) # Input
    y = torch.randn(N, D_out) # Label
    model = torch.nn.Sequential(
        torch.nn.Linear(D_in, H),
        torch.nn.ReLU(),
        torch.nn.Linear(H, D_out),
    )
    lr = 1e-6
    for t in range(500):
        # Forward Pass
        y_pred = model(x)
        loss = torch.nn.functional.mse_loss(y_pred,y)
        # BackPropagation
        loss.backward()
        # Weight update
        with torch.no_grad():
            for param in model.parameters():
                param -= lr * param.grad
        model.zero_grad() # Reset grad. for next iteration

~~별로 안 간단해 보이는 건 기분 탓인가~~

Reference

강의 및 그림 출처 1 (http://cs231n.stanford.edu)

[그림 출처 2] 2022 Fall EE488(B) DL for CV Lecture Note (by Prof. Jung)

Twitter Facebook LinkedIn